The root is the inverse operation to the exponentiation. In other words, the square root is a factor of a number which will become the original number when multiplied by itself. For example, the square root of  is
is  but if
but if  is multiplied by itself, it will result in the original number (which is
is multiplied by itself, it will result in the original number (which is  ). Another example is
). Another example is  , the square root of
, the square root of  is
is  but if
but if  is multiplied by itself then it will result in the original number (which is
is multiplied by itself then it will result in the original number (which is  ). Given two numbers, called the radicand and index, find a third number, which is called the root, such that when elevated to the index, it is equal to the radicand.
). Given two numbers, called the radicand and index, find a third number, which is called the root, such that when elevated to the index, it is equal to the radicand.

The index for the square root is  , although in this case it is omitted. Let's come back to all previous examples and describe them. In the first example, the number is
, although in this case it is omitted. Let's come back to all previous examples and describe them. In the first example, the number is  and the index will be
and the index will be  , radicant will be
, radicant will be  and the root will be
and the root will be  . In the case of the second example, the number is
. In the case of the second example, the number is  and the index is the same (which is
and the index is the same (which is  ). The radicant will be
). The radicant will be  and the root will be
and the root will be  .
.

The index usually defines how many times the number should be multiplied to get the original number. In the above examples, the index was taken  that means the number should be multiplied twice by itself to get the original number. Here is a new example with a different index, let's say you are asked to find
that means the number should be multiplied twice by itself to get the original number. Here is a new example with a different index, let's say you are asked to find 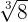 which means you need to find three factors. If we multiply
which means you need to find three factors. If we multiply  three times, it will end up
three times, it will end up  hence
hence 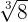 is
is  .
.
In simple words, the square root of a number, a, is accurate when a number is found, b, which when elevated to the square is equal to the radicand: 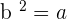

Exact square root
An exact square root has the remainder 0.
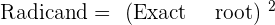

Perfect Square
These are the numbers that have exact square roots.
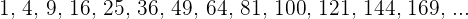
Not exact square root
If a number is not a perfect square, the square root is no exact.
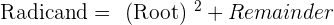

Summarise with AI:













I’m afraid this article (on cardinal numbers) has an unfortunate error. Zero must be considered a cardinal number. The definition of a cardinal number given by the Penguin Dictionary of Mathematics is “A number that indicates the number of elements in a set.” It also defines a null set or empty set containing no elements. The cardinality of this set is 0.