Chapters

Exercise 1
Calculate the value of y.
1 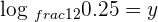
2 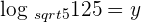
3 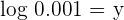
4 
5 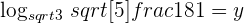
Exercise 2
Apply the definition of logarithms and calculate the value of x:
1 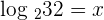
2 
3 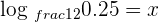
4 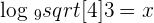
5 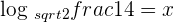
6 
7 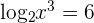
Exercise 3
Knowing that  , calculate the following logarithms.
, calculate the following logarithms.
1 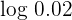
2 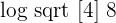
3 
4 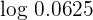
Exercise 4
Calculate:
1 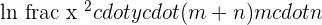
2 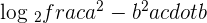
3 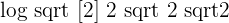
Exercise 5
Using logarithms, calculate the value of x.
1 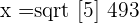
2 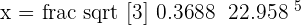
3 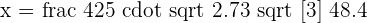
Solution of exercise 1
Calculate the value of y.
1 
Covert it into the exponential form like this:
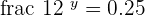
Since, 0.25 is equal to the square of 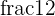 , hence
, hence 
So the final answer is 
2 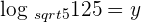
Convert it into the exponential form like this:

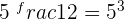
Hence, 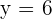
3 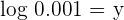
Convert it into the exponential form. Since it has no base, so we will assume that it is a common algorithm with base 10:
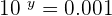
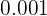 can be written as
can be written as 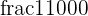 or
or 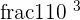 . According to the negative exponent rule, we can move the base to the numerator and the sign of 3 will change from positive to negative.
. According to the negative exponent rule, we can move the base to the numerator and the sign of 3 will change from positive to negative.
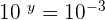
Hence, 
4 
Convert it into the exponential form like this:
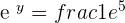
Apply the negative exponent rule, to write the right hand side of the equation in numerator:

Hence, 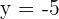
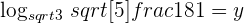

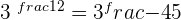 Multiply the exponents of both sides by 2 to get the value of
Multiply the exponents of both sides by 2 to get the value of  Hence,
Hence, 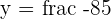
Find a good maths tutor near me here.
Solution of exercise 2
Apply the definition of logarithms and calculate the value of x:
1 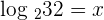
Convert the above logarithmic equation into the exponential form like this:
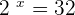
Since 2 raised to the power 5 is equal to 32, so we can write the equation as:
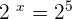

2 
Convert the above logarithmic equation into the exponential form like this:

Since 3 raised to the power 2 is equal to 9 and the fraction is equal to the negative power in the numerator, so we can write the expression as:
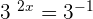
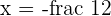
3 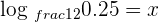
Convert the equation into exponential form like this:

Hence, 
4 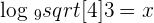
Convert the logarithmic form into an exponential form like this:
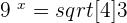
Since 3 raised to the power 2 is equal to 9 and the radical can be written in fractional exponential form, so the expression will be:
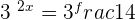
Hence, 
5 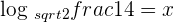
Convert the above logarithmic equation into the exponential form like this:

The radical form can be written in fractional exponential form like this:

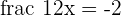
Multiply 2 on both the sides of the equation to get the final answer:
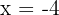
6 
Convert the above logarithmic equation into an exponential form like this:

It can be written into the fractional form like this:

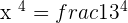
Hence, 
7 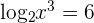
It can be written in exponential form like this:
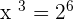
If 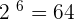 , then
, then 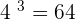 .
.
Hence, 
Solution of exercise 3
Knowing that log 2 = 0.3010, calculate the following logarithms.
1 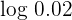
Since  can be written in the fractional form
can be written in the fractional form 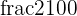 , hence we will write the above logarithmic function as:
, hence we will write the above logarithmic function as:

Apply the logarithm quotient rule here:
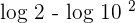
Apply logarithm power rule here:
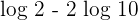
Since, 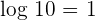 , so the resultant expression will be written like this:
, so the resultant expression will be written like this:
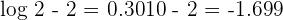
2 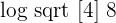
Applying the logarithm root rule here we get the following expression:
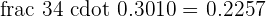
3 
It can be written as:
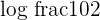
Applying the logarithm quotient rule here, we will get the following expression:

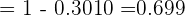
4 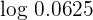
The above logarithm can be written in the fractional form like this:

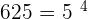 and 10000 can be written as a product of 2 and 4 raised to the power 4 like this:
and 10000 can be written as a product of 2 and 4 raised to the power 4 like this:

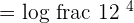
Apply the logarithm quotient rule here to get the following expression:
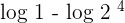
Since, log 1 =0 and the root rule can be applied to  , so we can write the expression as:
, so we can write the expression as:

Solution of exercise 4
Calculate:
1 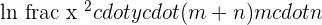
Apply the logarithm quotient rule here to get the following expression:
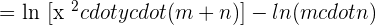
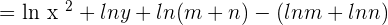
Simplify the expression and apply logarithm power rule here:
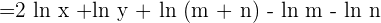
2 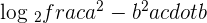
The formula in the numerator can be written as the product of two factors like this:
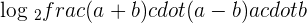
Applying the logarithm quotient rule here, we will get the following expression:
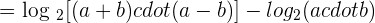
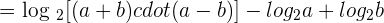
3 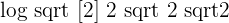
The above expression can be written as follows after applying the logarithm product rule:
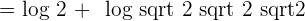
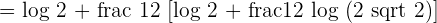
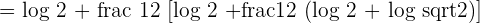
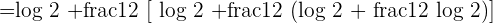
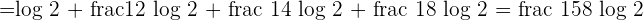
Solution of exercise 5
Remember that if you are asked to write the answers in numbers, then you can use your calculators to compute the final value of the variable. On the other hand, if you are asked to simplify the expression, you can simply apply the logarithm rules and write the simplified form of the expression.
In these exercises, we are asked to compute the value of  , so we have to write the answer in digits.
, so we have to write the answer in digits.
Using logarithms, calculate the value of x.
1 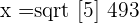
Take log on both sides of the equation. The resultant equation will be like this:
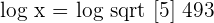

Calculate the antilogarithm.
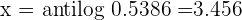
2 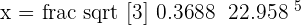
Take log on both sides of the equation to get the following expression:
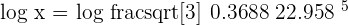
Apply the logarithm quotient rule here:

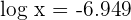
Take anti -log here:
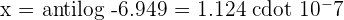
3 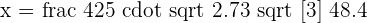
Take log on both sides of the equation to get the following expression:

Apply the logarithm quotient rule here to get the following expression:
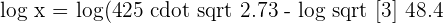
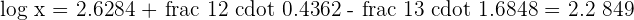
Take anti log here to isolate the variable  on the left hand side of the equation:
on the left hand side of the equation:
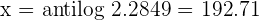













Totally helpful
Some of the equations are not readable (where a dividing liine is used) plus I found one mistake (ln42 instead of ln2)
So I think you should check the page: algebra/ log/ëxponential-equations-worksheet.
Exercise 1.4: I read that as 4^(x-1)^(1/2) – 2(x-1)^(1/2) – 2 = 0. But your solution does not make sense to me.
So probably you mean 4^(x-1)^(1/2) – 2^(x-1)^(1/2) – 2 = 0. But then your solution still does noet make sense to me. If the answer x = 3 then 16 -4 -2 = 10 (not 0).
Exercise 1.1 2^1 – x^2 = 1/8 is not correct. I haven’t looked at the other exercises yet. Please correct your mistakes.