Chapters
Exercise 1
Solve the exponential equations:
1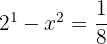 
2 
3 
4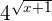 
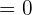
5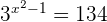 
6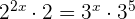 
7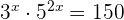 
Exercise 2
Solve the following exponential equations.
1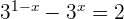 
2 
3 
4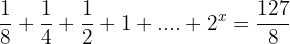 
5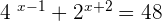 
Exercise 3
Solve the following exponential simultaneous equations.
1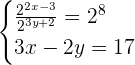 
2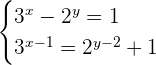 
3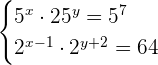 
Solution of exercise 1
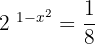
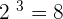, hence we can write 
on the right side of the equation 
: 
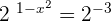
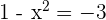
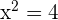
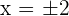
2
We can write the expression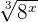 
as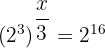 
The resulting expression after simplifying will be:
Cancel 2 from both sides of the equation to get the following answer:
3
We can write the above expression as:
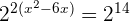
Cancel 2 from both sides of the equation to get:
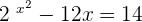
Divide both sides by 2 and set the equation equal to 0 by taking the constant to the right side of the equation:
Factor the equation like this:
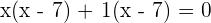
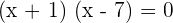
Either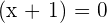 
or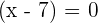 
Hence, 
or 
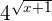
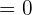
, hence we can write the equation like this: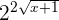
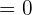Cancel 2 from both sides of the equation to get the following expression: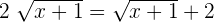 
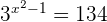
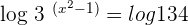
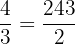
Take log on both sides of the equation:
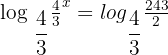
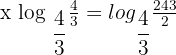
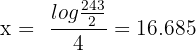
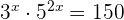
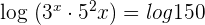
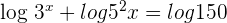
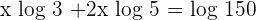
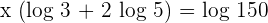
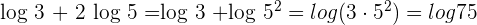
Solution of exercise 2
Solve the following exponential equations.
1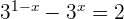
Suppose 
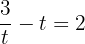
Solve the expression by taking L.C.M of the left hand side:
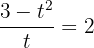
Set the equation to 0 by taking the constant to the left hand side of the equation:
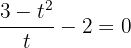
Simplify it further to get the following expression:
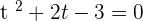
Find factors of the above expression like this:
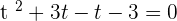
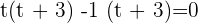
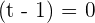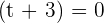
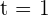or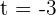 
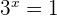or 
or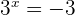 
The solution for 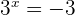cannot be determined, hence the exponential equation will have only one solution, i.e. 
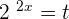
Solve the above expression by factoring like this:
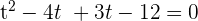
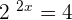
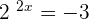
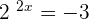has no solution.
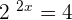has the solution which is 
3
We can write the above expression like this:
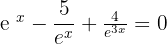
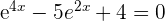
Put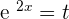 
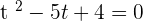
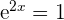
4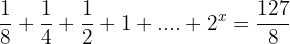
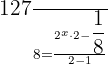
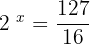
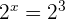
5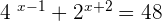
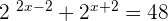
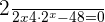
Suppose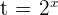 
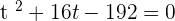
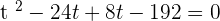
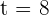or 
Solution of exercise 3
Solve the exponential simultaneous equations.
1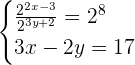
First, we will simplify the first expression and convert it into linear equation in two variables.
Take the expression 
from the denominator on the left hand side to the right hand side. Hence, the resultant equation will be:
Now, solve the system of linear equations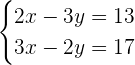 
Solving the system of linear equations we get the following values for 
and 
and 
2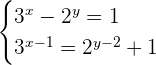
The second expression can be written as:
Put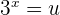 
and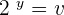 
The resultant system of equations will be:
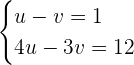
Solve the above system of linear equations to get the value of u and v:
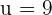and 
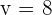
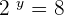
and 
and 
3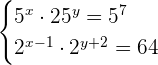
Since 
and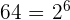 
, hence we can write the second expression as:
Simplifying both the equations further we will get:
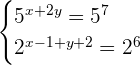
and 
You could check for reputable maths tutors here.
Did you like this article? Rate it!
Loading...
Totally helpful
Some of the equations are not readable (where a dividing liine is used) plus I found one mistake (ln42 instead of ln2)
So I think you should check the page: algebra/ log/ëxponential-equations-worksheet.
Exercise 1.4: I read that as 4^(x-1)^(1/2) – 2(x-1)^(1/2) – 2 = 0. But your solution does not make sense to me.
So probably you mean 4^(x-1)^(1/2) – 2^(x-1)^(1/2) – 2 = 0. But then your solution still does noet make sense to me. If the answer x = 3 then 16 -4 -2 = 10 (not 0).
Exercise 1.1 2^1 – x^2 = 1/8 is not correct. I haven’t looked at the other exercises yet. Please correct your mistakes.