Chapters

Introduction to Logarithms
Before proceeding to the logarithmic equations, let us see what are logarithms. Logarithms are actually another way of writing the exponential functions. You know that in exponential functions the independent variable is an exponent or power. The exponential function 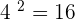 means
means  raised to the power
raised to the power  is equal to
is equal to  . In logarithmic form, it is written as
. In logarithmic form, it is written as 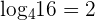 which means log of 16 with base 4 is equal to 2.
which means log of 16 with base 4 is equal to 2.
Remember that the base of a logarithm cannot be equal to 0. Since any number raised to the power 0 is equal to 1, so when it is converted in the logarithmic form, it will be written as  . When you use a calculator to compute
. When you use a calculator to compute  the answer is zero. The logarithms of 0 and negative numbers do not exist.
the answer is zero. The logarithms of 0 and negative numbers do not exist.
Logarithmic Equations
You are already familiar of the fact that the purpose of equations is to find the values of unknown variables. There may be a single or more than one variable in an equation. Depending on their form, equations are classified as linear, exponential, quadratic and logarithmic equations. In this article, we will discuss how to solve logarithmic equations using the rules of logarithms.
There are two kinds of logarithmic equations. One type is where the logarithm is only on one side of the equation. These types of equations are simple and can be solved by converting them into the exponential form. Do you know how logarithmic and exponential equations are related to each other? Well, the answer is straightforward. Both equations are inverses of each other. But the interesting fact is that the bases of both functions are the same.
For example, consider the following logarithmic equation:
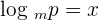
Convert the above equation into the exponential form like this:

You can see that the base of the logarithmic function is  and the base of its corresponding exponential function is also
and the base of its corresponding exponential function is also  .
.
The second type of equations has the logarithm on both sides of the equations. For example, consider the following example:
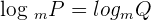
Since the above logarithmic equation has a single logarithm and the same base on both sides of the equations. So, the log functions will be canceled and the resulting equation will look like this:

Remember that if there are more logarithmic functions on one side than others, then even if they contain the same base, you cannot cancel the log functions. Instead, you need to apply the logarithmic rules to simplify the side which contains more than one log functions and then cancel the log function on both sides, given they have the same bases. These concepts will be clarified, as we will go through a couple of examples in this article.
Find a good maths tutor near me here.
Logarithmic Rules
Like exponent rules, there are some logarithmic rules which are used while solving logarithmic equations. The following table summarizes some of the logarithmic rules.
| Logarithm Rules | Mathematical Notation |
|---|---|
| Logarithm product rule | |
| Logarithm quotient rule | |
| Logarithm power rule | |
| Logarithm base switch rule | |
| Logarithm root rule | |
| Logarithm change of base rule |
Example 1
Solve the logarithmic equation 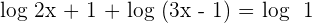
Solution
In the above example, there are three log functions. To solve the logarithmic equations, we should have 2, so we will use logarithm product rule on the left hand side of the equation to make it a single logarithm. Remember that we assume that a logarithmic function with no base is a common logarithm having a base 10.
In the above example, there are no bases on either side of the equation, so we have assumed that the logarithms on both sides have the same base 10.
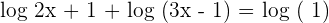

We will remove the log function from both sides of the equation and solve for the resulting equation:
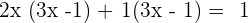
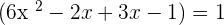
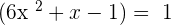
Set the equation to 0, by taking 1 to the right hand side of the equation:
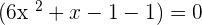
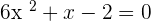
Now, we will factor the above algebraic expression by first expanding it and then finding the common factors from the pairs like this:
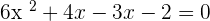
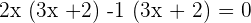
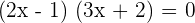
Either 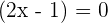 or
or 
If 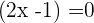 then
then 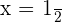 . If
. If 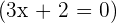 , then
, then 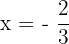 .
.
You can see that we have got one positive and one negative number as a solution. We will exclude the negative number 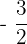 from the solution because when we will substitute this negative value in the original equation, we will end up taking the logarithm of a negative number.
from the solution because when we will substitute this negative value in the original equation, we will end up taking the logarithm of a negative number.
Hence, the only solution we are considering here is  .
.
Verification
Let us verify our solution by plugging this value of  in the equation
in the equation 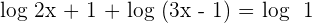 .
.
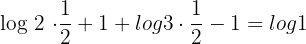
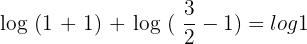
According to the logarithmic product rule, 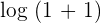 can be written as
can be written as 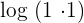 . According to the logarithmic quotient rule
. According to the logarithmic quotient rule 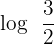 can be written as
can be written as 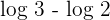 .
.
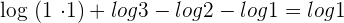

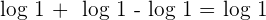
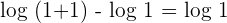

We need to transform the expression on the left hand side of the equation into a single logarithmic function.
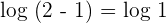
Cancel the log functions from both the sides of the equation to get the following algebraic expression:
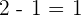
Hence, it is verified that  is a solution to the logarithmic equation.
is a solution to the logarithmic equation.
Example 2
Solve the logarithmic equation 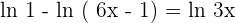
Solution
Apply the logarithmic quotient rule here, to transform the difference 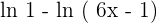 into a fractional form like this:
into a fractional form like this:
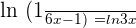
Since logs on both sides of the equations have same bases, so we will cancel out the log functions and write the expression algebraically like this:
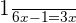
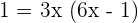
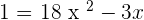
Set the equation equal to 0 by taking the terms on the right hand to the left hand side of the equation.

Find factors of the above expression by expanding it first, and then pairing it to find the common factors:

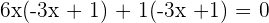
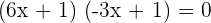
Either 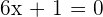 or
or  . Hence,
. Hence,  or
or 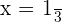 .
.
Since one solution is positive and the other is negative, so we will consider only the positive solution for the equation which is 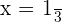 .
.
Verification
By putting 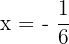 in the original equation, we will end up taking the logarithm of a negative number which is not possible, so we will exclude
in the original equation, we will end up taking the logarithm of a negative number which is not possible, so we will exclude 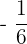 from the solution.
from the solution.
Put 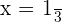 into the original equation to verify your answer.
into the original equation to verify your answer.
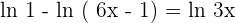
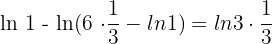

Applying the quotient rule here will give us the following logarithmic function:
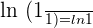
The log functions on both the sides will cancel each other, so the resultant algebraic expression will be written as:
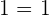
Hence, it is proved that  is the solution to the logarithmic equation.
is the solution to the logarithmic equation.
So far we have solved the equations which had logarithm with each number on both sides of the equations. Now, we will solve another type of equations which do not have the logarithm with each number.
Example 3
Solve the equation 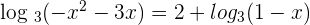
Solution
Take the logarithmic expressions to the left hand side of the equation:

We will apply logarithm quotient rule here and write the expressions on the left hand side as a single logarithm like this:
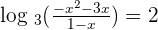
Convert the above logarithmic function into an exponential form:
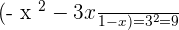
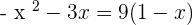
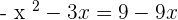
Set the equation equal to 0 by taking the expressions from the right hand side to the left hand side of the equation:
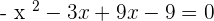
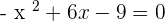
Factor the above expression by expanding it:

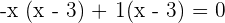
Either 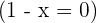 or
or 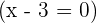 . Hence,
. Hence,  or
or  .
.
We need to check whether  and
and  are the solutions to the logarithmic equation or not.
are the solutions to the logarithmic equation or not.
Verification
We will do the verification of the above problem differently than others because the equation also had the constant on one side with the log functions with the same bases on both sides of the equation.
Let us verify our solution by plugging  and
and  in the original equation.
in the original equation.


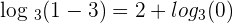
So, by plugging  in the solution we get negative numbers in the logarithms, so this cannot be the solution.
in the solution we get negative numbers in the logarithms, so this cannot be the solution.

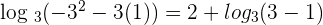

So, when we substitute 3 in the above equation, we got all positive numbers in the logarithms, so this is the solution to the equation.
Example 4
Solve the logarithmic equation 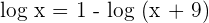
Solution
Take the log function from the right hand side of the equation to left hand side:
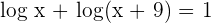
Apply the logarithm product rule on the left hand side of the equation:
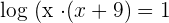

Since we can assume that a log function with no base is the common log function with base 10, so we will write the above function in exponential form like this:
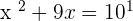
Set the equation equal to 0 by taking  on the left hand side of the equation:
on the left hand side of the equation:
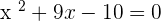
Factor the above expression by expanding it:
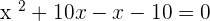
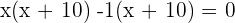
Either 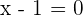 or
or 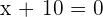 . Hence,
. Hence,  or
or 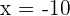 .
.
Verification
We cannot plug 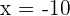 in the equation because when we do this, we will end up taking the logarithm of a negative number. We cannot take logarithms of negative numbers and 0, so
in the equation because when we do this, we will end up taking the logarithm of a negative number. We cannot take logarithms of negative numbers and 0, so 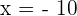 is not the solution to the equation. Let us plug the other solution which is
is not the solution to the equation. Let us plug the other solution which is  :
:
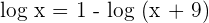

Apply the logarithm product rule here to write the expression like this:
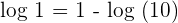
Since the constant is involved so we cannot cancel the log functions on both sides of the equations, but we can say that  is the solution to the equation because after substituting it in the original equation, we do not get the logarithms of a negative number or zero.
is the solution to the equation because after substituting it in the original equation, we do not get the logarithms of a negative number or zero.













Totally helpful
Some of the equations are not readable (where a dividing liine is used) plus I found one mistake (ln42 instead of ln2)
So I think you should check the page: algebra/ log/ëxponential-equations-worksheet.
Exercise 1.4: I read that as 4^(x-1)^(1/2) – 2(x-1)^(1/2) – 2 = 0. But your solution does not make sense to me.
So probably you mean 4^(x-1)^(1/2) – 2^(x-1)^(1/2) – 2 = 0. But then your solution still does noet make sense to me. If the answer x = 3 then 16 -4 -2 = 10 (not 0).
Exercise 1.1 2^1 – x^2 = 1/8 is not correct. I haven’t looked at the other exercises yet. Please correct your mistakes.