Chapters
In this article, we will discuss what are exponential equations, exponent rules, and how to solve exponential equations. Let us start with the definition of an exponential equation.
If "a" is a number given that it is greater than 0 and not equal to 1, then the equation in exponential form is written as:
, where
and
Here, "a" is known as the base of the equation which is a constant and x is the exponent or index of the base a.
You must have noticed that the independent variable "x" in the above exponential equation appears as an exponent. Now, the question arises that why we avoid the values 0 and 1. Well, let us substitute these values in the above equation to find out.


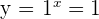
You can see that if the value of the base is 0 or 1, we get the answer 0 and 1 respectively. This is the reason we avoid 0 and 1 as values of "a".

Properties of Exponential Functions
Like all other equations, the exponential functions have certain properties that make them unique. These properties are discussed below:
- When you graph an exponential function in an x-y plane, then no matter what is the value of the base, the coordinates (0, 1) will be always included in the graph.
- For every value of "a",
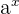 is greater than 0. In other words, we can say that
is greater than 0. In other words, we can say that 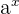 should not be zero.
should not be zero. - If the base of the exponential equation is greater than 0 but less than 1, i.e., 0 < a < 1, then the graph of such an exponential equation
 will decrease from left to right [see figure 1.1 which shows the graph of the function
will decrease from left to right [see figure 1.1 which shows the graph of the function  ].
]. - If the base of an exponential function is greater than 1, i.e.
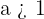 , then the graph of such an equation will increase from left to right [see figure 1.2 which shows the graph of the function
, then the graph of such an equation will increase from left to right [see figure 1.2 which shows the graph of the function  ].
]. - If
 , then
, then 


The inverse of exponential functions are logarithmic functions. For instance, consider an exponential function  . The inverse of this exponential function will be
. The inverse of this exponential function will be 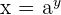 . In logarithmic form, this inverse will be written as:
. In logarithmic form, this inverse will be written as:
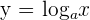
Just like exponential functions have properties that are discussed above, we also have properties of logarithms which are used to solve a logarithmic equation.
In the next section, we will discuss exponent rules.
Exponent Rules
Some rules of exponents are discussed below:
- Product Rule:
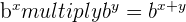
- Quotient Rule:
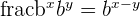
- Power Rule:

- Power of Product Rule:
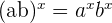
- Power of Fraction Rule:

- Zero Rule:

- Negative Exponent:

- Fractional Exponent:

In the next section, we will solve some examples in which we will use the exponent rules to solve exponential equations.
Find various Maths tutor on Superprof.
Example 1
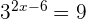
Solution

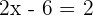

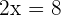

Example 2
Solve the equation 
Solution
According to fractional exponent rule, the function in this example can be written as:
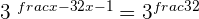
Since the bases on the left and right hand side of the exponential expressions are the same, hence we can write them as:


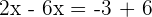


Example 3
Solve the equation 
Solution
We will use the exponent product rule here and rewrite the this equation as:
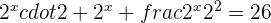


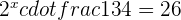
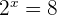
Substitute 8 2ith 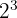 to get the following expression:
to get the following expression:
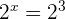
Since the left and right hand sides of the equation have same bases, hence we can write the exponents as:

Example 4
Solve the equation 
Solution
To solve this equation, we will take log on both sides of the equation:
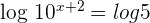

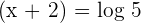
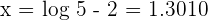
Example 5
Solve the equation 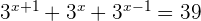
Solution
We will use the exponent product rule here and rewrite the this equation as:


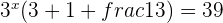
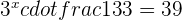

Substitute 9 with with  to get the following expression:
to get the following expression:
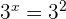
Since the left and right hand sides of the equation have same bases, hence we can write the exponents as:

Example 6
Solve the following exponential equation for the value x:

Solution
64 can be written as 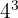 . Hence, we will substitute it in the above equation:
. Hence, we will substitute it in the above equation:
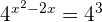
Since the left and right hand sides of the equation have same bases, so we can write the exponents as a new equation:

We will move the constant to the left hand side of the equation and set the equation equal to zero to convert the above equation into a standard form of a quadratic equation:

Now, we will factor the above equation to get the possible values of x. To factor, we need to expand the middle term -2x in such a way that the product of two terms is equal to 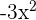 and the sum or difference is equal to -2x.
and the sum or difference is equal to -2x.
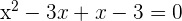

Set each factor equal to zero and solve new equations for x:
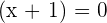

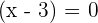

Hence, the values of x that satisfy the above equation are -1 and 3.
Example 7
Solve the following exponential equation for the value x:

Solution
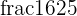 can be written as
can be written as  . Hence, we will substitute it in the above equation:
. Hence, we will substitute it in the above equation:
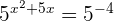
Since the left and right hand sides of the equation have same bases, so we can write the exponents as a new equation:

We will move the constant to the left hand side of the equation and set the equation equal to zero to convert the above equation into a standard form of a quadratic equation:

Now, we will factor the above equation to get the possible values of x. To factor, we need to expand the middle term 5x in such a way that the product of two terms is equal to  and the sum or difference is equal to 5x.
and the sum or difference is equal to 5x.


Set each factor equal to zero and solve new equations for x:
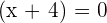
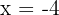
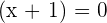

Hence, the values of x that satisfy the above equation are -1 and -4.
You could check for reputable maths tutors here.
Summarise with AI:














Totally helpful
Some of the equations are not readable (where a dividing liine is used) plus I found one mistake (ln42 instead of ln2)
So I think you should check the page: algebra/ log/ëxponential-equations-worksheet.
Exercise 1.4: I read that as 4^(x-1)^(1/2) – 2(x-1)^(1/2) – 2 = 0. But your solution does not make sense to me.
So probably you mean 4^(x-1)^(1/2) – 2^(x-1)^(1/2) – 2 = 0. But then your solution still does noet make sense to me. If the answer x = 3 then 16 -4 -2 = 10 (not 0).
Exercise 1.1 2^1 – x^2 = 1/8 is not correct. I haven’t looked at the other exercises yet. Please correct your mistakes.