In this article, we will learn exponential functions in detail. We will see how to construct a table of values of these mathematical functions and graph them using that table. We will also study properties of the exponential functions and solve word problems related to exponential growth and exponential decay. So, let us get started.
After linear functions, exponential functions are the most popular functions in mathematics which are also used in our daily life. For example, we use exponential functions to compute population growth or decline. In exponential functions, the independent variable  becomes an exponent. Mathematically, exponential equations are written as:
becomes an exponent. Mathematically, exponential equations are written as:
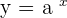 where
where  and
and 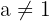
Here, a is the base of an exponential function,  is a dependent variable and
is a dependent variable and  is an independent variable. The base of an exponential function should be a positive number because a if the base is a negative number, it will unnecessarily complicate the function. Exponential functions are the inverses of logarithms. The fixed term
is an independent variable. The base of an exponential function should be a positive number because a if the base is a negative number, it will unnecessarily complicate the function. Exponential functions are the inverses of logarithms. The fixed term  is not equal to 1 or 0 because no matter what the value of
is not equal to 1 or 0 because no matter what the value of  is, they remain constant. It can be expressed as:
is, they remain constant. It can be expressed as:
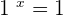
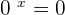 {where
{where  can be any value}
can be any value}
If you want to calculate the population growth, exponential function increases quickly. Similarly, if you are computing a population decline, exponential functions decrease swiftly.
Let us make the graph of the exponential functions. The parent exponential function is 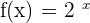 . The table of values for this exponential function is given below:
. The table of values for this exponential function is given below:
| x | y |
|---|---|
| -3 | 1/8 |
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
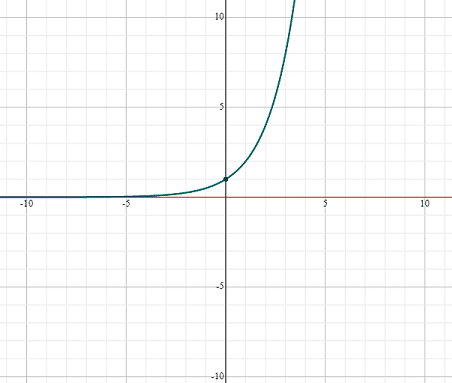

Properties of Exponential Functions
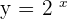 has the following properties:
has the following properties:- The point
 is the part of the graph which means that the graph passes through the point
is the part of the graph which means that the graph passes through the point 
- The domain of the exponential function having the base greater than 1 is equal to set of all real numbers
- The range of the exponential function having a base greater than 1 is set of all real numbers greater than 0. It means
 is equal to all positive real numbers.
is equal to all positive real numbers. - The graph increases and is asymptotic to the negative side of the
 -axis as
-axis as  approaches
approaches 
- The graph increase without limit as
 approaches
approaches 
- The graph of such exponential function is smooth and continuous
So far, we have discussed the graph and properties of the exponential function having the base greater than 1. Now, we will see what the properties of the exponential functions are if their base is less than 1. Let us consider an exponential function 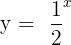 . The table of values of this exponential function is given below:
. The table of values of this exponential function is given below:
| x | y |
|---|---|
| -3 | 8 |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | 1/2 |
| 2 | 1/4 |
| 3 | 1/8 |
The graph of this exponential function is given below:
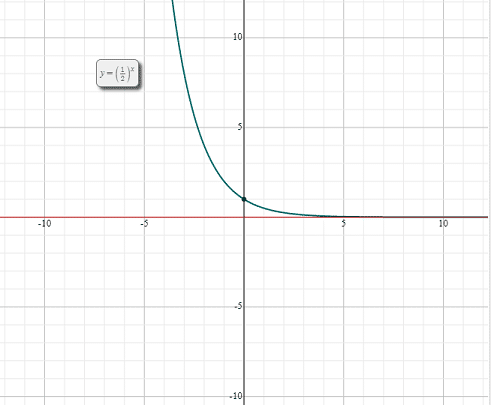
Now, you can tell the difference between the exponential functions with base greater than and less than 1. The properties of exponential functions having base less than 1 are given below:
Properties of Exponential Function when the base is less than 1
- Point
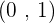 is part of the graph which means that the graph passes through the point (0,1)
is part of the graph which means that the graph passes through the point (0,1) - The domain of this exponential function is also equal to set of all real numbers
- The range of this exponential function is all positive real numbers, i.e.
 . Again, this property is the same for both types of exponential functions
. Again, this property is the same for both types of exponential functions - The graph decreases and is asymptotic to the positive side of
 - axis as
- axis as  reaches
reaches 
- The graph increases without limit as
 reaches
reaches 
- The graph of this exponential function is also smooth and continuous
- The graph is asymptotic to the x-axis as x approaches to infinity
Get more information about Maths tuition here.
Examples
Example 1
Now, we will see how we can graph exponential functions other than the parent exponent function. Consider the following example having a base greater than 1.

To graph this function, first we need to construct a table of values for this function. Remember that this is not a simple exponential function. You need to be careful in calculating the  values because the operation
values because the operation  is involved.
is involved.
| x | y |
|---|---|
| -2 | 1/3 |
| -1 | 1 |
| 0 | 3 |
| 1 | 9 |
| 2 | 27 |
Now, that we have obtained the table of values for the function, we can easily construct the graph by plotting the values in  plane.
plane.

Example 2
Now, we will see an example of an exponential function having base less than 1. Consider the following exponential function:
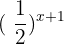
Before graphing this exponential function, we need to construct a table of values first like this:
| x | y |
|---|---|
| -2 | 2 |
| -1 | 1 |
| 0 | 1/2 |
| 1 | 1/4 |
| 2 | 1/8 |
Using the above table of values, we will construct the graph of an exponential function like this:
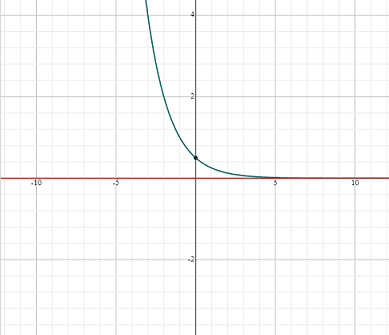
Exponential Functions Word Problems
We already have discussed in the article that the exponential functions are applicable to our daily lives. Let us see how to solve exponential growth and decay word problems.
Example 1
Sam bought a car of worth 15000 dollars. The car depreciates at an annual rate of 7%. What will be the price of car after six years?
Solution
The initial price of the car is 15000 dollars. The car depreciates at an annual rate of 7%, so 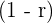 will be equal to
will be equal to 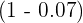 . Using this information, the exponential function will be written as:
. Using this information, the exponential function will be written as:
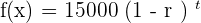

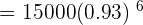
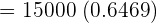
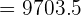
Hence, the price of the car after 6 years will be 9703.5 dollars.
Example 2
According to a census, the population of the city in 2014 was 150,000. The population is expected to increase by 11% annually. What will be the population of the city in 2019.
Solution
According to the above problem, we have got the following information:
Initial population of the city = a = 150,000
Annual increase in the population = r = 11% = 0.11
Number of years = t = 5
The function which will be used to compute the growth in the population is given below:
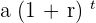
Solve this equation by plugging in the values from the problem:
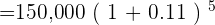


= 252,750
Hence, the population of the city after 5 years will be 252, 750.
Example 3
The half life of a radioactive element is 3.2 hours. If a scientist has 92 grams of the element now, how many grams will be left after 12.8 hours?
Solution
This is a half life problem and will solved differently than exponential growth and decline problems. We have obtained the following information from the above problem:
The half life of the radioactive element = 3.2 hours
Number of half lives = 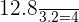
Take the exponent of  to compute the value which will be later by the initial amount to get the amount left after 12.8 hours.
to compute the value which will be later by the initial amount to get the amount left after 12.8 hours.
=  =
= 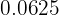
Number of grams left after 4 half lives = 
=  grams
grams
Hence, after 12.8 hours the scientist will have 5.75 grams of radioactive element.
Example 4
The half life of a radioactive element is 13 hours. If Sarah had 148 grams of the element now, how many grams will be left after 72 hours?
Solution
From the above problem, we have obtained the following information:
Half life of the radioactive element = 13 hours
Number of half lives will be calculated by dividing total hours passed by the half life of the radioactive element.
Number of half lives = 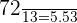
We need to multiply  5.53 times first using a calculator and then multiply the amount obtained with the initial amount of radioactive element to calculate the number of grams of radioactive element left in 5.53 half lives. To simplify, we have divided this final step into two parts.
5.53 times first using a calculator and then multiply the amount obtained with the initial amount of radioactive element to calculate the number of grams of radioactive element left in 5.53 half lives. To simplify, we have divided this final step into two parts.
= 
Number of grams left in 5.53 half lives = 148 . 0.0216
= 3.196 grams
Hence, after 72 hours 2.196 grams of the radioactive element will be left.
Example 5
The half life of a radioactive element is 7 hours. If George has 90 milli grams of radioactive element now, how many milligrams will be left after 33.6 hours
Solution
The information obtained from the above problem is below:
The original amount of the radioactive element = 90 milligrams
Number of hours passed = 33.6 hours
The half life of radioactive element = 7 hours
Number of half lives will be calculated by the time passed, i.e. 33.6 hours with the half life of the radioactive element which is 7 hours.
Number of half lives = 4.8
To calculate the amount left after 33.6 hours, first, we will multiply  4.8 times.
4.8 times.
= 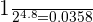
Now, we can easily calculate the amount left after 4.8 half lives have passed by multiplying the amount left after 33.6 hours by the initial amount George had.
Number of milligrams left after 4.8 half lives = 0.0358 . 90
= 3.22 milligrams
Hence, after 33.6 hours 3.22 milligrams of the radioactive element will be left.
Summarise with AI:













Totally helpful
Some of the equations are not readable (where a dividing liine is used) plus I found one mistake (ln42 instead of ln2)
So I think you should check the page: algebra/ log/ëxponential-equations-worksheet.
Exercise 1.4: I read that as 4^(x-1)^(1/2) – 2(x-1)^(1/2) – 2 = 0. But your solution does not make sense to me.
So probably you mean 4^(x-1)^(1/2) – 2^(x-1)^(1/2) – 2 = 0. But then your solution still does noet make sense to me. If the answer x = 3 then 16 -4 -2 = 10 (not 0).
Exercise 1.1 2^1 – x^2 = 1/8 is not correct. I haven’t looked at the other exercises yet. Please correct your mistakes.