
Exercise 1
Solve the logarithmic equations.
1 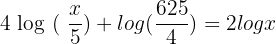
2 
3 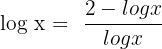
4 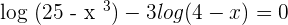
5 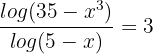
Exercise 2
Solve the logarithmic simultaneous equations.
1 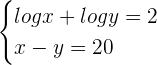
2 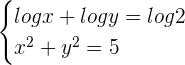
3 
Solution of exercise 1
Solve the logarithmic equations.
1 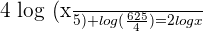
Applying the logarithmic power rule here, we will get the following expression:
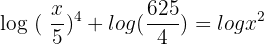
Write the two terms on the left hand side as a single log function by applying logarithm product rule:
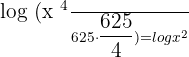
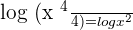
Since both sides of the equation has log functions, so you can write the resultant expression without them like this:
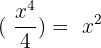
Set the equation equal to 0 by taking 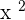 on the left hand side of the equation:
on the left hand side of the equation:
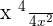
The above fraction can be written as:

Either 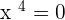 or
or 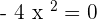
Hence,  ,
,  or
or 

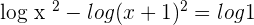

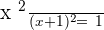
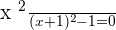

If we substitute 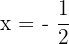 in the original equation, we will end up taking the log of negative number which is impossible. Hence, this equation has No Solution.
in the original equation, we will end up taking the log of negative number which is impossible. Hence, this equation has No Solution.
3 
By taking the factors from right hand side of the equation to the left hand side and setting the equation to 0, we will get the following expression:
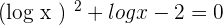
Suppose 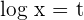
By substituting the  value in the equation, we will get the following new equation:
value in the equation, we will get the following new equation:
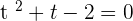
We will factor the above equation by expanding it and writing the factors in two pairs like this:
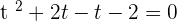
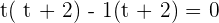
Either 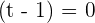 or
or 
Hence, t = 1 or t = -2
Remember that we assumed 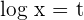 , hence we can say that
, hence we can say that 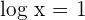 or
or 
By converting the above values in exponential form, we get the following values of  :
:
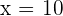 and
and 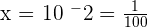
4 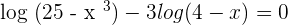
Apply the power rule here to write the equation as follows:
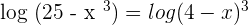
Cancel the log functions on both sides of the equation to get the following algebraic expression:

Use the formula to expand the right hand side of the equation:

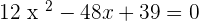

5 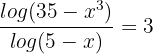
Take the expression from the denominator on the left hand side to the numerator on the right hand side of the equation:
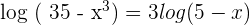
Apply the logarithm power rule here to get the following equation:

Cancel the log functions from both sides of the equation and solve the resultant equation algebraically:


Find factors of above expression by expanding it:
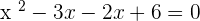
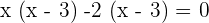
Hence,  or
or 
Solution of exercise 2
Solve the logarithmic simultaneous equations.
1 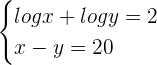
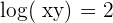

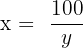
 in the second equation:
in the second equation: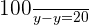
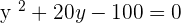
 :
: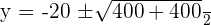


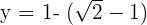

2 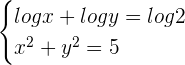
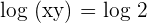 Cancel the log function from both sides of the equation:
Cancel the log function from both sides of the equation: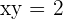
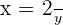

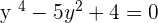
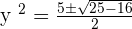
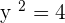 and
and 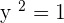 Hence,
Hence, 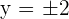 or
or 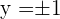
If  , then
, then 
If  then
then 
3 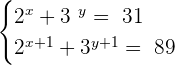
We can rewrite the second equation using the exponent product rule:
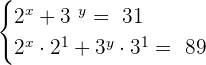
Suppose  and
and 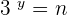
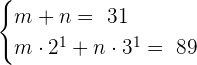
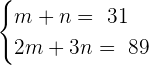
We will solve this equation through substitution:
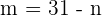
Substitute this value of  in the second equation:
in the second equation:


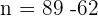
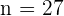
Put this value of  in the first equation to get the value of
in the first equation to get the value of  :
:
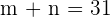
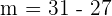

Remember that  and
and 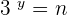
Hence,  and
and 
Since, 2 raised to the power 2 is equal to 4, so the value of  .
.
Similarly, 3 raised to the power 3 is equal to 27, so  .
.
Find a good maths tutor near me here.













Totally helpful
Some of the equations are not readable (where a dividing liine is used) plus I found one mistake (ln42 instead of ln2)
So I think you should check the page: algebra/ log/ëxponential-equations-worksheet.
Exercise 1.4: I read that as 4^(x-1)^(1/2) – 2(x-1)^(1/2) – 2 = 0. But your solution does not make sense to me.
So probably you mean 4^(x-1)^(1/2) – 2^(x-1)^(1/2) – 2 = 0. But then your solution still does noet make sense to me. If the answer x = 3 then 16 -4 -2 = 10 (not 0).
Exercise 1.1 2^1 – x^2 = 1/8 is not correct. I haven’t looked at the other exercises yet. Please correct your mistakes.