Chapters
To learn about logarithmic functions, first, recall exponential functions because logarithmic functions are the inverses of the exponential functions. The general form of the exponential function is  , where a represents the base and
, where a represents the base and  represents the power.
represents the power.
The inverse of  is
is 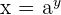 . The expression
. The expression 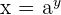 . is equivalent to
. is equivalent to 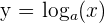 , where
, where  and
and 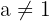 . In words, we can describe it as the logarithm of
. In words, we can describe it as the logarithm of  to the base
to the base  is
is  . Keep in mind that it is not possible to take the logarithm of a negative number or 0.
. Keep in mind that it is not possible to take the logarithm of a negative number or 0.
For example, consider the simple exponential function 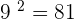 . In words, we can say that nine raised to the power 2 is 81. Now, we will see how to write this function in logarithmic form and say in words.
. In words, we can say that nine raised to the power 2 is 81. Now, we will see how to write this function in logarithmic form and say in words.
In the logarithmic form, we can write this expression as  . In words, we can describe it as the logarithm of 81 to the base 9 is 2. In the following table, we have written some common functions in exponential and logarithmic forms.
. In words, we can describe it as the logarithm of 81 to the base 9 is 2. In the following table, we have written some common functions in exponential and logarithmic forms.
| Exponential form | Logarithmic form |
|---|---|
From the above table, we can conclude that the base of exponential and its corresponding logarithmic function is the same.

Natural and common logarithms
Natural logarithms are logarithmic functions with base e. Natural log is expressed as

Common logarithms are the logarithmic functions with base ten. They are expressed as follows:
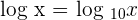
Before proceeding to the graphs of logarithmic functions, we will evaluate some logarithmic functions first in the following examples.
Example 1

Solution
We will solve the above expression in multiple steps.
Step 1 – Convert in exponential notation
Suppose 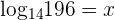 . First, express this function in exponential notation:
. First, express this function in exponential notation:
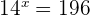
Step 2 – Solve for x
The exponent we require on 14 to get 196 as an answer is 2, hence 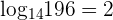 .
.
Example 2
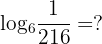
Solution
Step 1 – Convert in exponential notation
Suppose 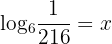 .
.
Convert the above function in exponential form:
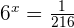
Step 2 – Solve for x
We know that when an exponent is negative, then final answer is a fraction. In the above example, the exponent must be negative because the answer 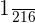 is in fractional form. If the exponent of 6 is 3, we get the answer 216. If the exponent is -3, we will get
is in fractional form. If the exponent of 6 is 3, we get the answer 216. If the exponent is -3, we will get 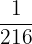 .
.
Example 3
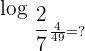
Solution
Step 1 – Convert in exponential notation
Suppose 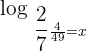 . First, convert the function in exponential form like this:
. First, convert the function in exponential form like this:
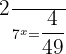
Step 2 – Solve for x
Since, 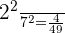 , so
, so 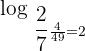 .
.
Example 4
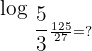
Solution
Step 1 – Convert in exponential notation
Suppose 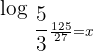 . Convert this logarithmic function into an exponential form like this:
. Convert this logarithmic function into an exponential form like this:
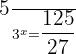
Step 2 – Solve for x
Since, 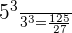 , so
, so 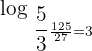
Characteristics of Logarithmic Functions Graphs
We know how to evaluate the logarithmic functions. Now, we will see how to plot logarithmic functions in a coordinate axis. But before proceeding to some examples, let us see what are some of the characteristics of graphs of the logarithmic functions. The graphs of all logarithmic functions will have the following characteristics:
- The graph of logarithmic functions passes through the points (1,0).
- If the base of a logarithmic function is greater than 1, then the graph increases
- If the base of the logarithmic functions is greater than 0 but smaller than 1, then the graph decreases.
- The domain of the logarithmic function is all numbers greater than 0.
- The range of logarithmic function is all real numbers
- Graph of these functions is asymptotic to the y-axis, i.e. it gets closer to the y-axis but never crosses it.
Example 1
Graph the function 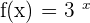 and is logarithmic form
and is logarithmic form  .
.
Solution
Step 1
We will construct two separate tables for both the functions. The table of values for the exponential function 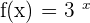 is given below:
is given below:
| x | f(x) |
|---|---|
| -2 | 1/9 |
| -1 | 1/3 |
| 0 | 1 |
| 1 | 3 |
| 2 | 9 |
Step 2
Plotting the above values in a coordinate axis will give the following graph of the exponential function:
Step 3
We know that the logarithmic functions are the inverses of exponential functions. So, the function 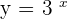 will be written as
will be written as 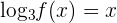 in logarithmic form. The table of this function is given below:
in logarithmic form. The table of this function is given below:
| x | f(x) |
|---|---|
| 1/9 | -2 |
| 1/3 | -1 |
| 1 | 0 |
| 3 | 1 |
| 9 | 2 |
Step 4
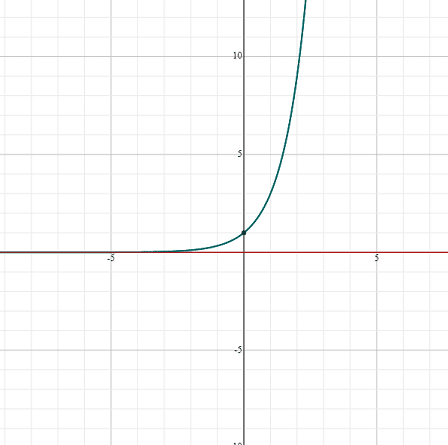
The graph of the logarithmic function is given below. You can see that this logarithmic graph is the flipped version of the exponential function graph.
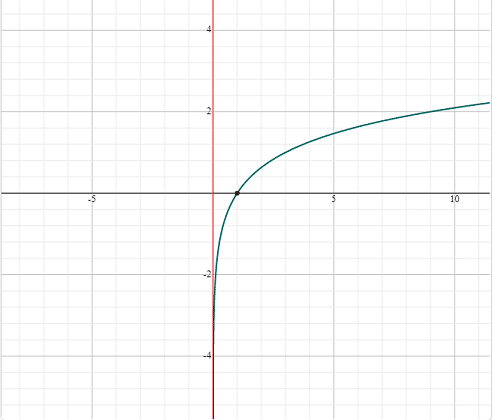
You can see that the above logarithmic graph satisfies all the properties of the logarithmic function graph. The above logarithmic curve passes through the points (1,0). Although it is near to the y-axis, however, it does not cross it. Since, the base of this logarithmic function was 3, i.e. greater than 1, so the graph is increasing.
You could check for reputable maths tutors here.
Example 2
Now, let see in another example what happens when the base of the logarithmic function is less than 1. Plot the graph of the function 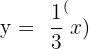 and its logarithmic form
and its logarithmic form 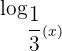 .
.
Solution
Step 1
To plot the graphs, first we need to construct the table of exponential function like this:
| x | f(x) |
|---|---|
| -2 | 9 |
| -1 | 3 |
| 0 | 1 |
| 1 | 1/3 |
| 2 | 1/9 |
Step 2
The graph of this function is given below.

Step 3
The table of values for the logarithmic function is given below.
| x | f(x) |
|---|---|
| 9 | -2 |
| 3 | -1 |
| 1 | 0 |
| 1/3 | 1 |
| 1/9 | 2 |
Step 4
The graph of the logarithmic function is given below.

Like all logarithmic functions, the above logarithmic curve passes through the points (1,0). It is also asymptotic to the y-axis, i.e. it gets very close to it, but never crosses it. From the above two examples we can conclude that whether the base of the logarithmic functions is greater than or less than 1, the general properties of logarithmic function graphs do not change. You can see that the graph is decreasing because the value of the base was less than 1.
Example 3
Graph the function 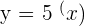 and its logarithmic form
and its logarithmic form  .
.
Solution
Step 1
Construct a table of the function 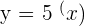 .
.
| x | f(x) |
|---|---|
| -2 | 1/25 |
| -1 | 1/5 |
| 0 | 1 |
| 1 | 5 |
| 2 | 25 |
Step 2
Plot the graph of the exponential function using the above table of values.

Step 3
We know that the logarithmic function is inverse of an exponential function, so we will reverse the values of  and
and  of the exponential table.
of the exponential table.
| x | f(x) |
|---|---|
| 1/25 | -2 |
| 1/5 | -1 |
| 1 | 0 |
| 5 | 1 |
| 25 | 2 |
Step 4
We will get the following graph by plotting the values in the  plane.
plane.

The above logarithmic curve passes through the points (1,0). It is also asymptotic to the y-axis, i.e. it gets very close to it, but never crosses it. Since, the base of this logarithmic function was 5, i.e. greater than 1, so the graph is increasing.
Summarise with AI:













Totally helpful
Some of the equations are not readable (where a dividing liine is used) plus I found one mistake (ln42 instead of ln2)
So I think you should check the page: algebra/ log/ëxponential-equations-worksheet.
Exercise 1.4: I read that as 4^(x-1)^(1/2) – 2(x-1)^(1/2) – 2 = 0. But your solution does not make sense to me.
So probably you mean 4^(x-1)^(1/2) – 2^(x-1)^(1/2) – 2 = 0. But then your solution still does noet make sense to me. If the answer x = 3 then 16 -4 -2 = 10 (not 0).
Exercise 1.1 2^1 – x^2 = 1/8 is not correct. I haven’t looked at the other exercises yet. Please correct your mistakes.