Chapters
- Adding Complex Numbers
- Properties of Complex Number Addition
- Commutative and Associative Properties
- Visualization of the Addition of Complex Numbers
- The Parallelogram Law for the Addition of Complex Numbers
- Adding Triangles
- Visualizing Adding 3 or more Vectors: Commutative Property
- Visualizing Subtraction of 2 Complex Numbers
- Subtraction is Addition of the Opposite of a Complex Number
- The Relationship Between a Complex Number and its Conjugate

Adding Complex Numbers
We add Complex numbers in a component-wise fashion exactly like vector addition, i.e. add the Real parts of each number together, the  components, and add the Imaginary parts of each number together, the
components, and add the Imaginary parts of each number together, the  components, to form a new Complex number with new Real and Imaginary parts
components, to form a new Complex number with new Real and Imaginary parts
If 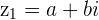 and
and 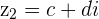 , then their sum is a new Complex number
, then their sum is a new Complex number  with
with 

where  is the
is the  and
and
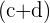 is the
is the 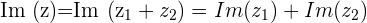 multiplied by
multiplied by  .
.
Notice that

Example
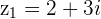 and
and 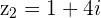 with
with 

Here  and
and 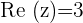 with
with 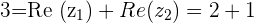 and
and
 with
with 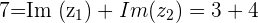
Point in the Complex Plane
Example
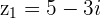 and
and 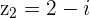 with
with 

Here 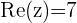 and
and 
The new number is associated with a point 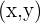
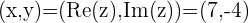
in the 2nd Quadrant of the Complex plane.
Properties of Complex Number Addition
Additive Identity
Example
 and
and  with
with 
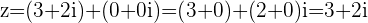
This shows that adding the Complex number 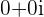 to any number gives us back that number.
to any number gives us back that number.
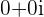 is known as the Additive Identity of the Complex Numbers.
is known as the Additive Identity of the Complex Numbers.
Additive Inverse
Example
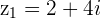 and
and  with
with  then
then
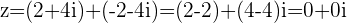
This shows that adding the negative of a Complex number to that number gives us back the Additive Identity.
The opposite or negative of a Complex number is that Complex number's Additive Inverse.
If 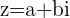 then
then 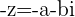 and
and
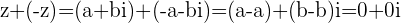
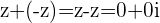
Adding Multiple Complex Numbers
Adding 3 or more Complex numbers is performed in the same manner. We just need to keep track of the components of each number
Ex. 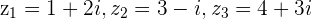 and
and 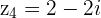 with
with 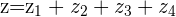 then
then
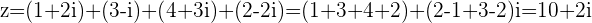
Subtracting Complex Numbers
We subtract one Complex number from the other by adding the opposite of the number we are subtracting
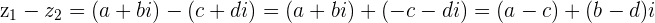
Example
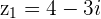 and
and  with
with  then
then
 z=(4-3i)-(3-2i)=(4-3)+(-3-(-2))i=1-i
z=(4-3i)-(3-2i)=(4-3)+(-3-(-2))i=1-i
Commutative and Associative Properties
The addition of Complex numbers follows the rules of Commutativity and Associativity for addition
Commutative Property: 
Example
 and
and 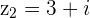
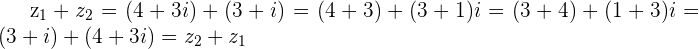
Associative Property: 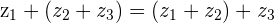
Example
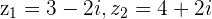 and
and 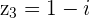 then
then

and
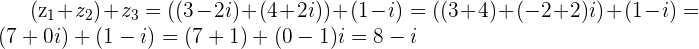
Visualization of the Addition of Complex Numbers
1-Dimensional Addition
We can look at the 1-Dimensional case of the addition or subtraction of Real Numbers on the number line for insights into what happens when we add or subtract vector quantities.
When we add or subtract Real numbers, we are taking an initial position, the first number, on the number line and moving the position to the right, by the addition of another number, or to the left, by the subtraction of another number. This is called displacement.
Distance between 2 Real Numbers
The distance between two numbers  and
and  on the Real Number Line is the absolute value of their difference
on the Real Number Line is the absolute value of their difference
 |x_2-x_1|=|x_1-x_2|
|x_2-x_1|=|x_1-x_2|
Distance between 2 Complex Numbers
The distance between 2 points 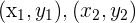 in the plane is found by the distance formula
in the plane is found by the distance formula
 d=sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}
d=sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}
Complex Numbers as a 2-Dimensional Displacement
One vector in the plane with coordinates 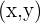 is a 2-Dimensional displacement from the origin. We are finding a spot in the plane that is a distance
is a 2-Dimensional displacement from the origin. We are finding a spot in the plane that is a distance
 sqrt{(x-0)^{2}+(y-0)^{2}}=sqrt{(x)^{2}+(y)^{2}}
sqrt{(x-0)^{2}+(y-0)^{2}}=sqrt{(x)^{2}+(y)^{2}}
from the origin.
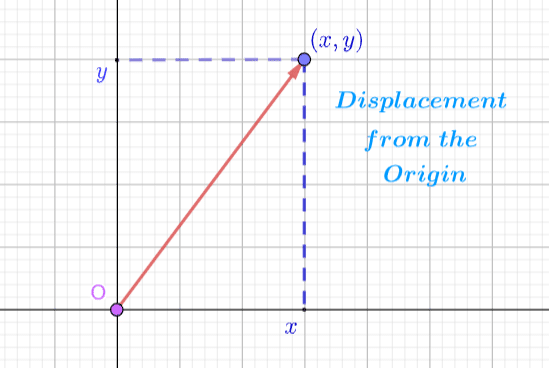
Points in the Complex Plane
A Complex number marks a point, which is a place in the plane that is perpendicular to both the  and
and  axes (unless it lies on one of the axes or the origin, in which case it is coincident with one or both axes and is only perpendicular to one of the axes or lies at the origin).
axes (unless it lies on one of the axes or the origin, in which case it is coincident with one or both axes and is only perpendicular to one of the axes or lies at the origin).
The Modulus of a Complex Number is the Hypotenuse of a Right Triangle
Perpendicularity allows us to make a right triangle and use the Pythagorean Theorem to find the modulus of the vector, the hypotenuse of the right triangle.
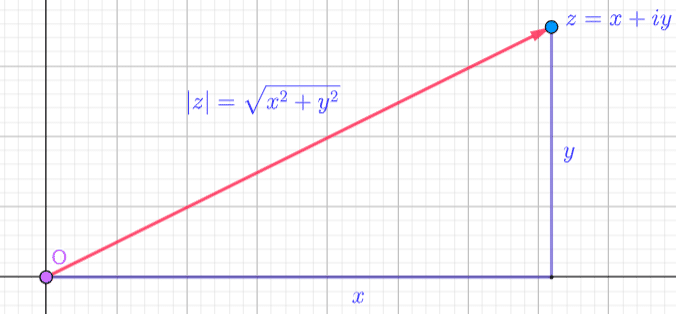
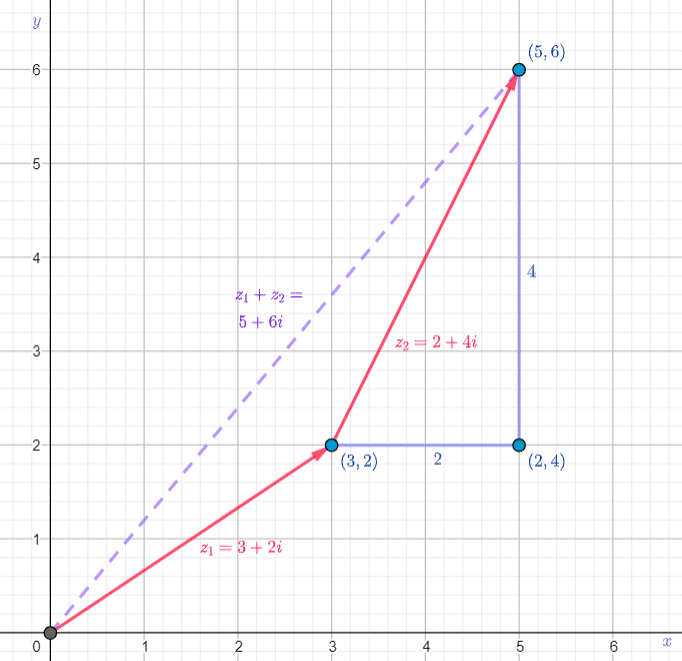
The Parallelogram Law for the Addition of Complex Numbers
Adding one Complex number to another Complex number is a 2-Dimensional displacement from the initial position of the first Complex number to the final position of the second Complex number.
We add the  components and the
components and the  components of the first and second number together to find a new place in the plane. This is displacement from an initial position to a new and final position, which is 2 total displacements from the origin.
components of the first and second number together to find a new place in the plane. This is displacement from an initial position to a new and final position, which is 2 total displacements from the origin.
The order that we add the 2 Complex numbers together is irrelevant. The end of the path we take to the new position is the same whether we traverse the first vector and then the second vector or vice versa.
This is known as the Parallelogram Law for Addition, showing that we have 2 different independent routes to get to the vector sum.
This is also a consequence of the Associativity of Complex number addition.
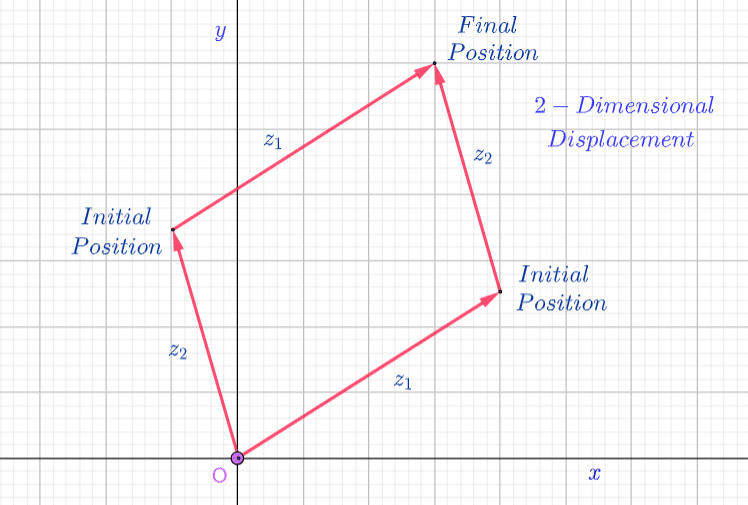
The new position is an end path that starts at the origin, goes to a new position and ends at the final position.
Example
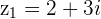 and
and 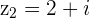 then
then
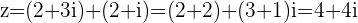

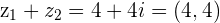 is the final position whether we travel to
is the final position whether we travel to 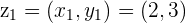 first and add
first and add 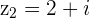 or we travel to
or we travel to 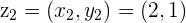 first and then add
first and then add 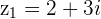
Adding Triangles
Finding the new position by adding a Complex number is equivalent to adding a right triangle, with sides equal to the  and
and  components and hypotenuse equal to the modulus of the second vector, to the tip of the initial vector
components and hypotenuse equal to the modulus of the second vector, to the tip of the initial vector
Example
 and
and 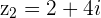 then
then
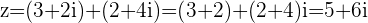
This is a 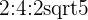 right triangle added to the tip of the initial Complex number at the point
right triangle added to the tip of the initial Complex number at the point 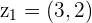
The point 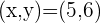 is a distance of
is a distance of

from the point 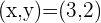
Triangle Inequality
The modulus of the Complex number  is
is
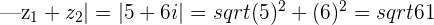
which is around 
and this is less than
 |z_1|+|z_2|=|3+2i|+|2+4i|=sqrt{(3)^{2}+(2)^{2}}+2sqrt{5}=
|z_1|+|z_2|=|3+2i|+|2+4i|=sqrt{(3)^{2}+(2)^{2}}+2sqrt{5}=
 sqrt{13}+2sqrt{5}
sqrt{13}+2sqrt{5}
which is around 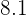
The modulus of the sum of 2 Complex numbers is always less than or equal to the modulus of the first number plus the modulus of the second number, with equality only holding when the 2 numbers are in a straight line
 |z_1+z_2|leq|z_1|+|z_2|
|z_1+z_2|leq|z_1|+|z_2|
This is the Triangle Inequality, where the sum of the lengths of any 2 sides of a triangle are greater than or equal to the length of the third side.
Visualizing Adding 3 or more Vectors: Commutative Property
Example
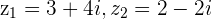 and
and 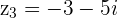 with
with 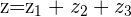
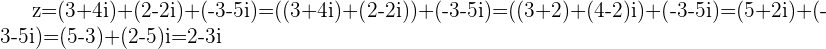
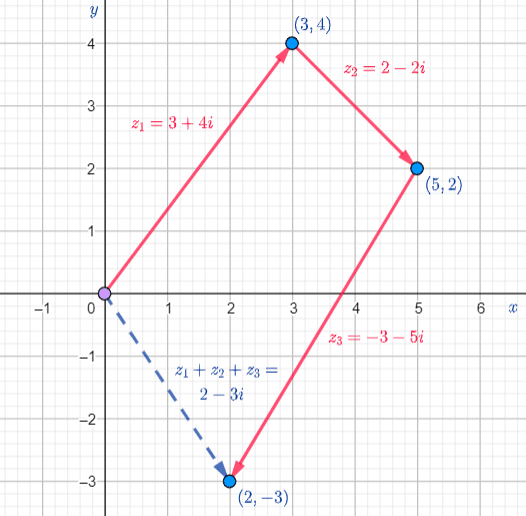
Notice that this is the same sum as if we would add the vector  to the vector
to the vector 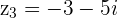
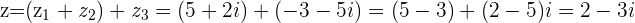
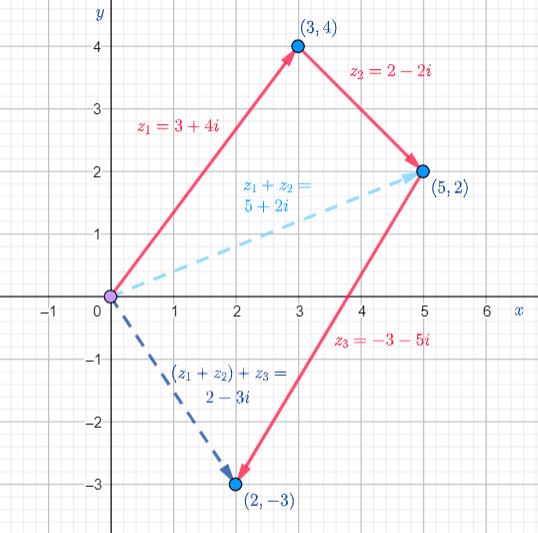
and also the same sum if we would add vector  to the vector
to the vector 

This shows that the Commutative Property holds true. The final sum is independent of the path taken.
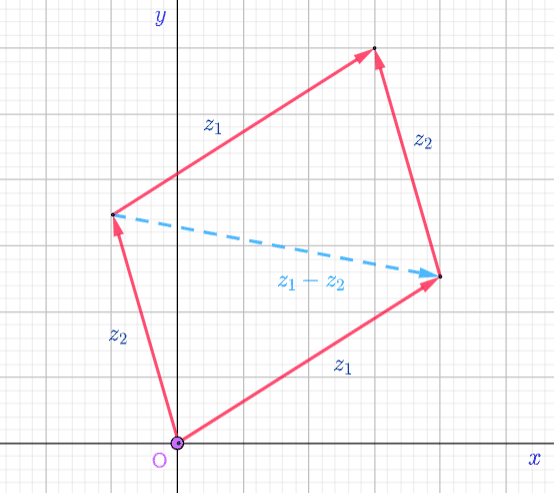
Visualizing Subtraction of 2 Complex Numbers
When we subtract Complex numbers, we are subtracting components from each other, instead of adding them.
Using the parallelogram form we used before for Complex addition, we can see that the other diagonal connecting the vectors  and
and  gives the vector
gives the vector  directed towards
directed towards 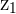 or the vector
or the vector  directed towards
directed towards 
Example
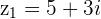 and
and 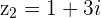 with
with 
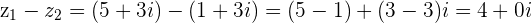

The number 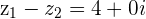 is directed towards the point
is directed towards the point 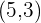 because we are subtracting
because we are subtracting  from
from 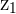 .
.
Subtraction is Addition of the Opposite of a Complex Number
Example
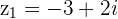 and
and 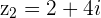 , then its negative is
, then its negative is 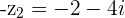
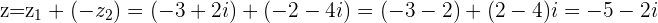

 is the blue dotted line, while
is the blue dotted line, while 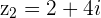 , the negative of
, the negative of  is the green dotted line and the sum of
is the green dotted line and the sum of 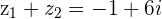 is the purple dotted line
is the purple dotted line
We can see that adding the negative of a Complex number is similar to the subtraction of the original Complex number but the vector is directed towards  instead of
instead of 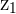 .
.
The Relationship Between a Complex Number and its Conjugate
Real and Imaginary Parts of a Complex Number
We will show that  and
and 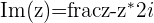
Example
 and
and 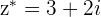 with
with 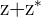
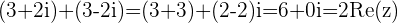
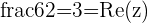
so 
Example
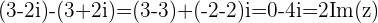

so 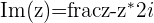
Conjugate of a Sum is the Sum of the Conjugates
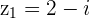 and
and  with
with 

then 
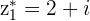 and
and 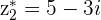
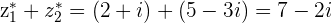 and
and
 z^{*}=(z_1+z_2)^{*}=z_1^{*}+z_2^{*}
z^{*}=(z_1+z_2)^{*}=z_1^{*}+z_2^{*}
This shows that the conjugate of the sum of 2 Complex numbers is equal to the sum of the conjugates of each Complex number.
Summarise with AI:













It is a good for me for giving some help in order to understand very well
this qwestion is necessary
l need support for complex numbers , inverse of quadratic equation, set theory