Powers of Complex Numbers Introduction
We can find powers of Complex numbers, like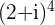
, by either performing the multiplication by hand or by using the Binomial Theorem for expansion of a binomial
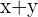. This can be somewhat of a laborious task. Fortunately, there is a nifty shortcut that we can apply to shorten the process and it involves the Polar form of Complex numbers.
Example
Find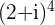
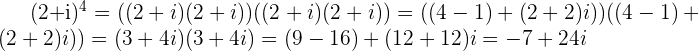
with a modulus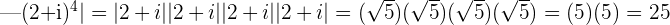
which equals
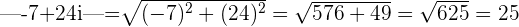
Powers of the Polar Form
We saw in the Polar Representation section the proof that
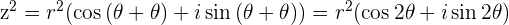
and we're going to extend this definition to show that the power of any Complex number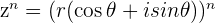
also has a very special and useful result.
Example
We'll extend the result for
and apply it to
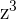
If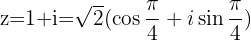
with
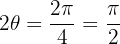then
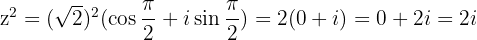
then
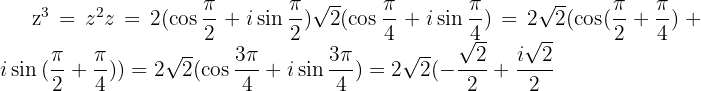
Example
If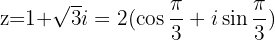
with
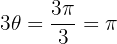then
We can now infer that
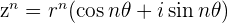
De Moivre's Theorem and The Unit Circle
By setting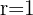
and using the Unit Circle, we obtain De Moivre's Theorem
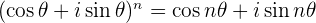
This is an extremely useful theorem for finding powers and roots of Complex numbers. We can express the sine or cosine function of a multiple of an angle
,
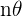, by powers of the sine and cosine of the original angle
. We do this by applying the Binomial Theorem for a power
to the product
.
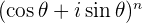Example
If
then we can expand the right side in powers of the sine and cosine of
by using the binomial expansion for
Binomial Expansion for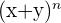
:
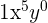
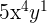
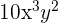
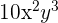
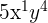
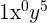
for decreasing powers of cosine from
and increasing powers of sine from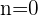
then
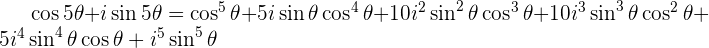
The Real part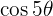
of the expansion is
and the Imaginary part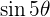
of the expansion is
Summarise with AI:
Did you like this article? Rate it!
Loading...
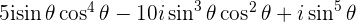
It is a good for me for giving some help in order to understand very well
this qwestion is necessary
l need support for complex numbers , inverse of quadratic equation, set theory