Chapters
In this article, we will discuss what are imaginary and complex numbers, how powers are applied to imaginary numbers, and how to multiply and divide complex numbers. Let us start with the imaginary numbers first.
Find more Maths tuition here on Superprof.

What are Imaginary Numbers?
Imaginary numbers are also referred to as complex numbers and they are the product of the real numbers, let say "a" and the imaginary unit "i". Mathematically, they are written as follows:
Imaginary Number =
Here, "a" is a real number and "i" is an imaginary unit.
The symbol "i" is used to denote the imaginary unit in mathematics. In mathematical notation, an imaginary unit is written as a square root of -1.
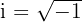
If 2 is multiplied by this imaginary unit "i", then we can write it as 2i or 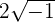 . The square of an imaginary number is a negative number. For example, the square of "i" is equal to the
. The square of an imaginary number is a negative number. For example, the square of "i" is equal to the 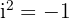 .
.
Imaginary numbers are very useful in mathematics because they make those problems easier to explain that involve the square root of a negative number. The imaginary numbers are not tangible, i.e., they do not possess a tangible value, therefore they are neither classified as a real number nor they can be represented on a number line. For instance, the square root of - 36 is 6i.
What are Complex Numbers?
Remember that complex numbers are different from imaginary numbers. They are of the form 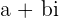 , where a and b are real numbers. The complex numbers have two parts, a and bi. The "a" part of the complex numbers is the real number part and the "bi" part of the complex numbers is an imaginary part.
, where a and b are real numbers. The complex numbers have two parts, a and bi. The "a" part of the complex numbers is the real number part and the "bi" part of the complex numbers is an imaginary part.
Applications of Imaginary Numbers in Other Fields
Classified as complex numbers, the imaginary numbers are used in many other fields besides mathematics:
- They are widely used in electricity and quadratic equations. In electronics, they are represented by the symbol j because i in electronic denotes current. These numbers are especially used in AC (Alternating Current) electronics.
- During a sine wave, AC changes from positive to negative and negative to positive. The imaginary and real numbers help in AC electricity calculations.
- These numbers are also applicable in signal processing. Signal processing plays a vital role in cellular, wireless, and radar technologies.
- These numbers are extremely useful in number theory, geometry, physics, and engineering too.
Powers of the Imaginary Unit
The powers of imaginary units are explained below:
The values are repeated in groups of four, therefore, to know the value of a particular power of i, divide the exponent by 4, and write the number as:
 .
.
Here, Q represents the quotient and R represents the remainder.
For instance, consider an imaginary number 
When 22 is divided by 4, we get the quotient 5 and remainder 2. It can be written mathematically as:
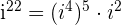
 is equal to 1 and
is equal to 1 and 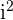 is equal to -1:
is equal to -1:


Now, let use consider another example 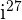 . When 27 is divided by 4, we get the quotient 6 and the remainder 3. Mathematically, we can write it as:
. When 27 is divided by 4, we get the quotient 6 and the remainder 3. Mathematically, we can write it as:
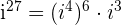
 is equal to 1 and
is equal to 1 and  is equal to - i:
is equal to - i:
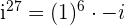

In the next section, we will evaluate some expressions containing the imaginary numbers using the arithmetic operations of multiplication and division.
Example 1
Compute 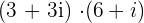 . Write the answer as complex number.
. Write the answer as complex number.
Solution
In this example, we will multiply two expressions like we multiply binomials.
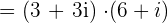
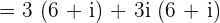
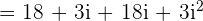
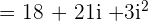
Our expression 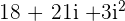 is not of the form
is not of the form 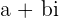 . It can be simplified further because
. It can be simplified further because 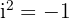
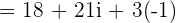
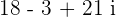

Example 2
Evaluate  . Write the answer as complex number.
. Write the answer as complex number.
Solution
We will multiply two expressions like we multiply binomials to simplify the expression in this example:
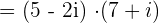
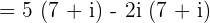

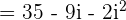
Our expression  is not of the form
is not of the form 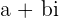 . It can be simplified further because
. It can be simplified further because 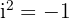
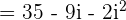
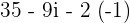
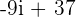
Example 3
Evaluate 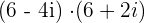 . Write the answer as complex number.
. Write the answer as complex number.
Solution
Just like binomial expressions, the first expression will be multiplied by the second one:
 .
.
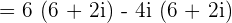


Our expression  is not of the form
is not of the form 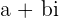 . It can be simplified further because
. It can be simplified further because 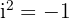


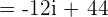
Example 4
Evaluate  . Write the answer as complex number.
. Write the answer as complex number.
Solution
Just like binomial expressions, the first expression will be multiplied by the second one:
 .
.
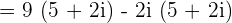

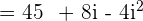
Our expression  is not of the form
is not of the form 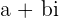 . It can be simplified further because
. It can be simplified further because 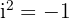

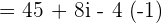
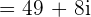
Example 5
Solve the expression 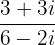
Solution
To solve the division involving complex numbers, we use conjugates. To take the conjugate, change the sign between expressions in the denominator. The conjugate of 6 - 2i is 6 + 2i. Now, we will multiply and divide the expression by the conjugate like this:
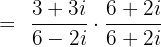
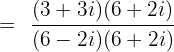

Substitute 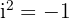 in the above expression:
in the above expression:
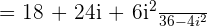


Simplifying the above expression will give us the following answer:

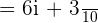
It can be simplified further like this:
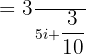
Example 6
Simplify the expression 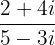
Solution
Since this example involves complex numbers, therefore we will use conjugates. To take the conjugate, change the sign between expressions in the denominator. The conjugate of 5 - 3i is 5 + 3i. Now, we will multiply and divide the expression by the conjugate like this:
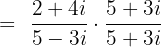
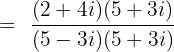

Substitute 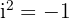 in the above expression:
in the above expression:

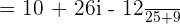

Simplifying the above expression will give us the following answer:
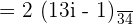

It can be simplified further like this:
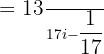
Example 7
Simplify the expression 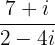
Solution
Division of the complex numbers is completed by taking conjugate of the denominator. To take the conjugate, change the sign between expressions in the denominator. The conjugate of 2 - 4i is 2 + 4i. Now, we will multiply and divide the expression by the conjugate like this:
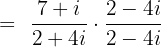
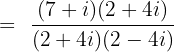

Substitute 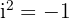 in the above expression:
in the above expression:
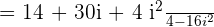
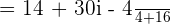

Simplifying the above expression will give us the following answer:


It can be simplified further like this:
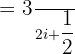










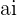
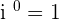

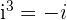
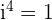



It is a good for me for giving some help in order to understand very well
this qwestion is necessary
l need support for complex numbers , inverse of quadratic equation, set theory