Chapters
- Introduction
- Complex Multiplication Laws
- Real and Imaginary Number Multiplication
- Multiplicative Identity and Multiplicative Inverse
- Conjugate Multiplication and the Modulus
- Equations with Complex Solutions
- Visualization of Complex Number Multiplication
- Multiplication is Angle Addition
- Triangle Method

Introduction
We multiply 2 Complex numbers 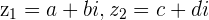 with
with 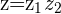 by treating each of them as binomials and using the normal form of binomial multiplication, the FOIL process (First, Outer, Inner, Last)
by treating each of them as binomials and using the normal form of binomial multiplication, the FOIL process (First, Outer, Inner, Last)
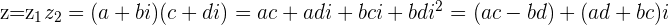
with  which makes
which makes 
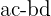 is the Real part of the product
is the Real part of the product 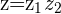 or
or 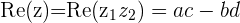
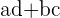 is the Imaginary part of the product
is the Imaginary part of the product 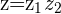 or
or  multiplied by
multiplied by 
Example
 and
and 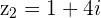 with
with 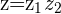
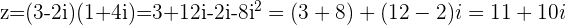
or straight into 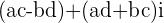 form
form
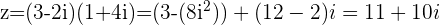
The 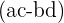 form already takes into account that there will be an
form already takes into account that there will be an  term, which will make
term, which will make 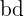 the opposite sign of the original product.
the opposite sign of the original product.
Example
 and
and 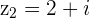 with
with 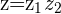
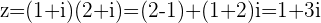
Complex Multiplication Laws
Commutative Law

Example
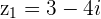 and
and 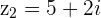 then
then

Associative Law
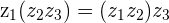
Example
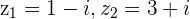 and
and 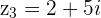 then
then
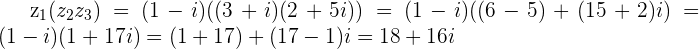
and
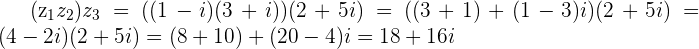
Multiplying 3 or more Complex numbers is the same process as 2 number multiplication, just with extra steps.
Distributive Law

Example
 and
and 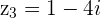 then
then
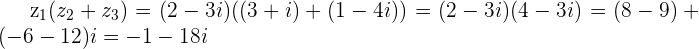
and
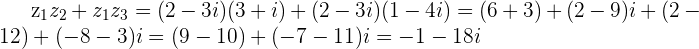
Real and Imaginary Number Multiplication
Real Multiplication
Multiplying a Complex number by a Real number 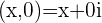 just magnifies or shrinks the components of the number by the magnitude of the Real number.
just magnifies or shrinks the components of the number by the magnitude of the Real number.
Example
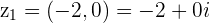 and
and 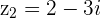 then
then
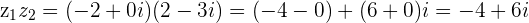
Multiplying a Complex number by  doubles the
doubles the  and
and  components and changes their sign.
components and changes their sign.
Example
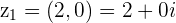 and
and 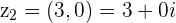 then
then
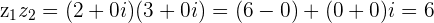
Multiplying 2 Real numbers together gives back a Real number as a product.
Imaginary Multiplication
Justification of 
Example
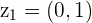 and
and  then
then
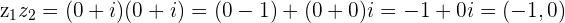
Example
Ex.  and
and 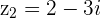 then
then
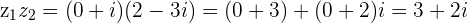
Multiplying a Complex number by an Imaginary number 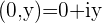 magnifies or shrinks the components by the magnitude of the Imaginary number, switches the magnitudes of the components and changes the sign of the y component.
magnifies or shrinks the components by the magnitude of the Imaginary number, switches the magnitudes of the components and changes the sign of the y component.
Multiplicative Identity and Multiplicative Inverse
Multiplicative Identity
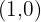 is the Multiplicative Identity of the Complex Numbers.
is the Multiplicative Identity of the Complex Numbers.
Example
 and
and 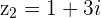 then
then
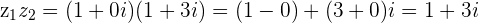
Multiplying a Complex number by  gives back the Complex number as the product.
gives back the Complex number as the product.
Multiplicative Inverse
The Multiplicative Inverse 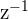 of a Complex number
of a Complex number  is
is

Example
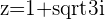 and
and 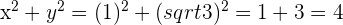 then
then
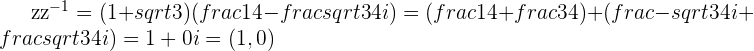
This shows that  gives back the Multiplicative Identity as the product.
gives back the Multiplicative Identity as the product.
Conjugate Multiplication and the Modulus
Conjugate Multiplication gives the Square of the Modulus
When we multiply a Complex number  by its conjugate
by its conjugate  , we obtain the square of the modulus
, we obtain the square of the modulus

of the Complex number  .
.
If  then
then  and
and
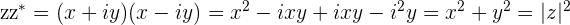
Example
 and
and 
The modulus of its conjugate 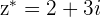 is also equal to
is also equal to 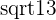
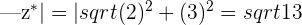
and 
then 
The Conjugate of a Product
The conjugate of the product of 2 Complex numbers is equal to the product of the conjugates of 2 Complex numbers.

Example
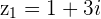 and
and 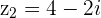 then
then z_1z_2=(1+3i)(4-2i)=(4+6)+(-2+12)i=10+10i
z_1z_2=(1+3i)(4-2i)=(4+6)+(-2+12)i=10+10i and
and 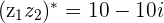
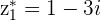 and
and  then
then
The Modulus of a Product
We want to show that the identity  holds true
holds true
Example
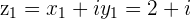 and
and 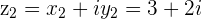 then
then
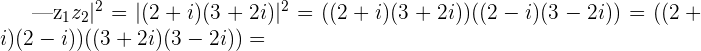

and then by taking the square root of both sides of the equation 
we can deduce that 
which is an important and useful identity that shows that the modulus of a product is equal to the product of each modulus.
Equations with Complex Solutions
We may encounter equations that involve the square of an unknown Complex number 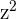 set equal to another known Complex number
set equal to another known Complex number 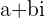 where we have to solve for the Complex number's Real and Imaginary parts
where we have to solve for the Complex number's Real and Imaginary parts
Example
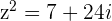 with
with  then
then
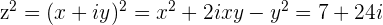
we set the Real part of 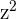 equal to
equal to  and the Imaginary part of
and the Imaginary part of 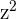 equal to
equal to 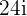 and have two equations
and have two equations
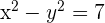 and
and 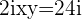 or
or 
we can solve for  and
and  by finding the modulus of
by finding the modulus of 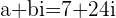
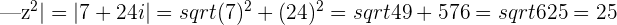
and by using the identity 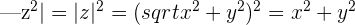
we can say 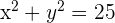 and use this to find
and use this to find  and
and 
 and
and

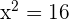 and
and 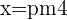
 and
and 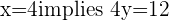 and
and 
then the first solution 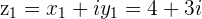
 and
and  and
and 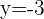
then the second solution is 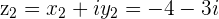
Checking the solutions
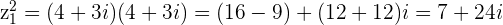
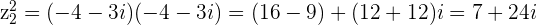
Visualization of Complex Number Multiplication
Introduction
Multiplication by  is a 90 degree rotation in the
is a 90 degree rotation in the  .
.
Multiplying a positive Real number by  switches the number from the positive
switches the number from the positive  to the positive
to the positive 
Example
 and
and 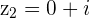 with
with 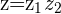

or just 
and multiplying a negative Real number by  switches the number from the negative
switches the number from the negative  to the negative
to the negative 
Multiplying a positive Imaginary number by  switches the number from the positive
switches the number from the positive  to the negative
to the negative 

Example
 and
and 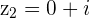
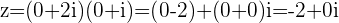
and multiplying a negative Imaginary number by  switches the number from the negative
switches the number from the negative  to the positive
to the positive 
Multiplying a Complex number by  switches the
switches the  and
and  components and changes the sign of the switching
components and changes the sign of the switching  component
component
Example

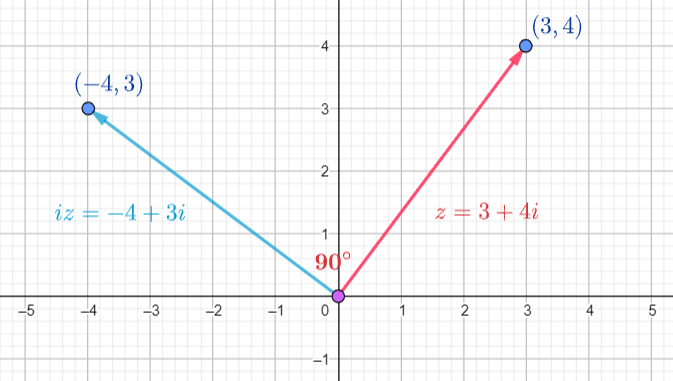
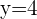 switches to
switches to 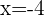 and
and  switches to
switches to 
Example
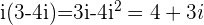
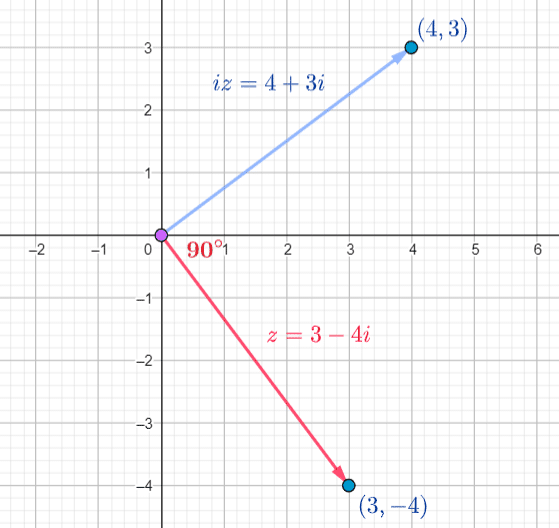
The product of the multiplication of 2 Complex numbers is another Complex number
Example
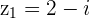 and
and  then
then
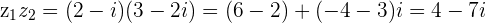

Multiplication is Angle Addition
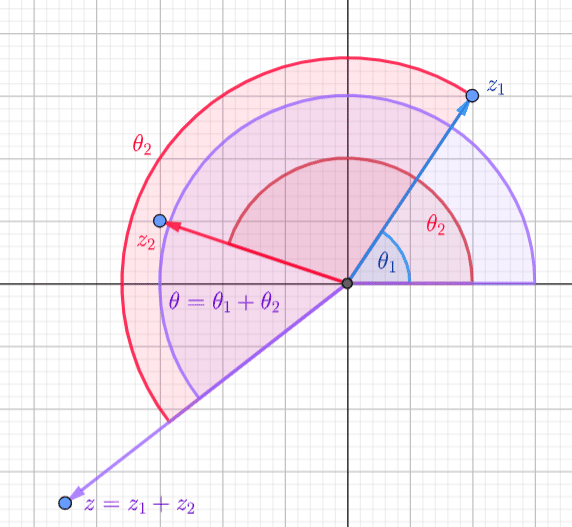
Triangle Method
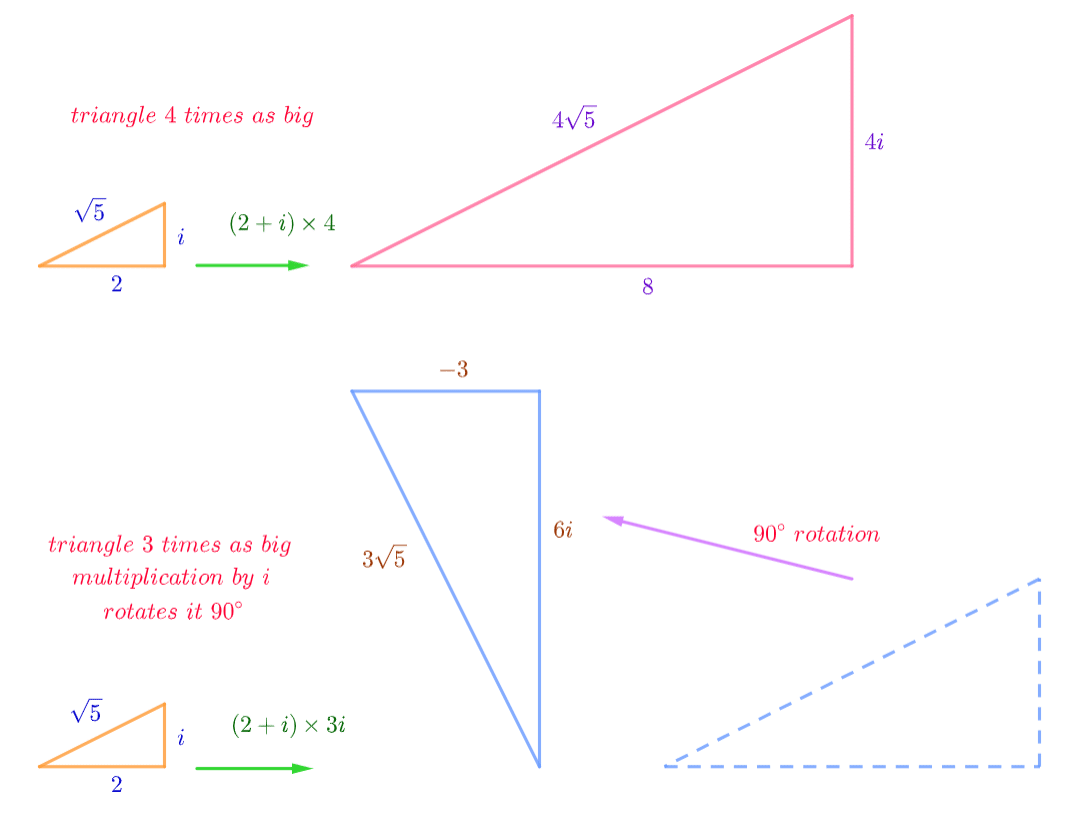













It is a good for me for giving some help in order to understand very well
this qwestion is necessary
l need support for complex numbers , inverse of quadratic equation, set theory