Chapters

Introduction
Division of Complex numbers is an undefined process by itself. There is no way to properly 'divide' a Complex number by another Complex number.
This means that if there is a Complex number that is a fraction that has something other than a pure Real number in the denominator, i.e. an Imaginary number or a Complex number, then we must convert that number into an equivalent fraction that we will be able to Mathematically manipulate.
When a Complex number appears in the denominator, we must rationalize the denominator to form an equivalent number that has a Complex number in the numerator only and a Real number in the denominator only.
We rationalize the denominator by multiplying both the top and the bottom of the fraction by the conjugate of the Complex number in the denominator, which is just equivalent to multiplication by 
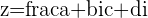 we must multiply it by
we must multiply it by 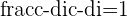
then

Example
If 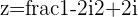 then the conjugate of the denominator is
then the conjugate of the denominator is 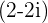 and
and
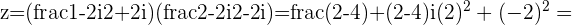

We turned an undefined operation of division problem into an equivalent multiplication problem by using the conjugate. Multiplying both the numerator and the denominator by the conjugate of the denominator makes the denominator the square of its modulus and the numerator a new Complex number. The new Complex number with just a Real number in the denominator is equivalent to the old Complex number because we only multiplied by an expression that is equivalent to  .
.
Example
 then
then

Example
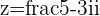 then
then
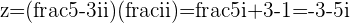
The Reciprocal of a Complex Number
If we have a certain Complex number  , we can find the value of its reciprocal
, we can find the value of its reciprocal 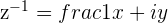 by rationalizing the denominator in the same way.
by rationalizing the denominator in the same way.
Example
If  with
with 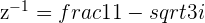 and
and 

This shows that 
meaning the reciprocal of a Complex number is equal to the conjugate of that Complex number divided by the square of the modulus. The inverse is a scaled version of the conjugate.
Visualizing the Division of Complex Numbers
The product of the division of a Complex numbers 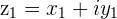 by another
by another 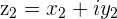 is a new, scaled Complex number that has a new angle
is a new, scaled Complex number that has a new angle 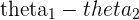 . The numerator
. The numerator 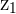 is multiplied by
is multiplied by 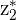 and the reciprocal of the squared modulus of the denominator
and the reciprocal of the squared modulus of the denominator  ,
, 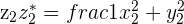 .
.
We subtract the angle during division because we are actually multiplying by the reflection of the denominator, which has an angle 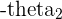 .
.
Example
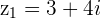 and
and  then
then
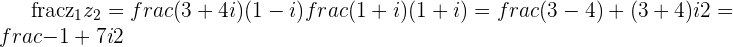
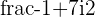 is a scaled by
is a scaled by 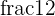 version of the regular product of
version of the regular product of


Modulus and Argument
Example
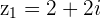 and
and  then
then
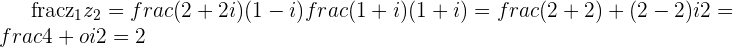
Dividing by  subtracts an angle of
subtracts an angle of 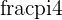 because
because 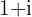 has an angle of
has an angle of 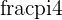 .
.
This shows that 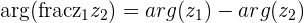
The new Complex number is located on the positive x-axis a distance of 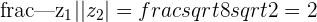 away from the origin.
away from the origin.
This shows that 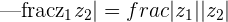
Example
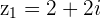 and
and  then
then
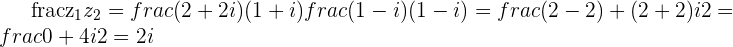
Dividing by 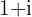 adds an angle of
adds an angle of 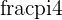 because
because  has an angle of
has an angle of 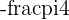 . The new Complex number is located on the positive y-axis a distance of
. The new Complex number is located on the positive y-axis a distance of 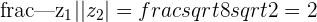 away from the origin.
away from the origin.
Summarise with AI:













It is a good for me for giving some help in order to understand very well
this qwestion is necessary
l need support for complex numbers , inverse of quadratic equation, set theory