Chapters

Square Roots of Complex Numbers
Square Roots of Real and Imaginary Numbers
Just as we can find powers of a Complex number, we can also find any roots of a Complex number by using their Polar representation.
Taking the square root (or any root) of a Real number is the process of finding a Real number whose square is equal to the original number.
Real numbers have 2 square roots, a positive solution and its negative
Example
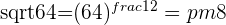
An Imaginary number has a positive and a negative square root
Example
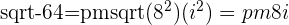
Square Root of a Complex Number z=x+iy
When we want to find the square root of a Complex number, we are looking for a certain other Complex number which, when we square it, gives back the first Complex number as a result.
Complex numbers have 2 square roots, a certain Complex number  and its opposite
and its opposite 
Existence of the Square Root
Example
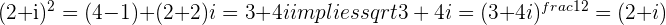
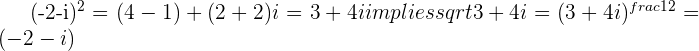
This shows the existence of the square roots of a Complex number, but does not actually show the process we would use to solve for them.
Polar Form and the Power Formula
To do that, we need to use the Polar form of the Complex number and the power formula

and not use the restriction that  be an Integer and open up its domain to include the Rational numbers
be an Integer and open up its domain to include the Rational numbers 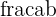
If we choose 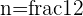 and use the power formula, we get
and use the power formula, we get
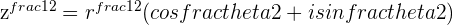
Example
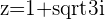 with
with  and
and 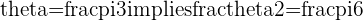
then

Square of the Opposite
If we square the opposite of the result  , we should get back
, we should get back 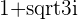
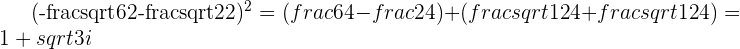
This shows that the 2 square roots are just opposites of each other  and
and 
nth Root of a Complex Number
We can extend our result for the power 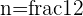 to include
to include 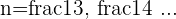 by using the formula
by using the formula

where  is one root out of the total for
is one root out of the total for 
If 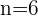 then
then  goes form
goes form  to
to 
The solutions are all located the same distance from the origin and are all separated by the same angle, not necessarily as measured from the positive x-axis, but from the vector representing one root to the vector representing the next root in line.
Geometrically, each 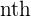 root of
root of  ,
,  , is an equally spaced point that forms the vertices of a regular polygon, i.e. each
, is an equally spaced point that forms the vertices of a regular polygon, i.e. each  root of a Complex number forms a vertex of a pentagon.
root of a Complex number forms a vertex of a pentagon.
Example
 and
and  then
then

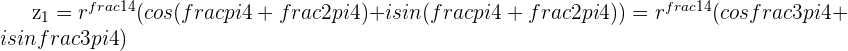


Example
We'll find the cube roots of 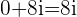 at an angle of
at an angle of 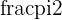

with 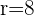 and
and 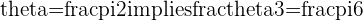

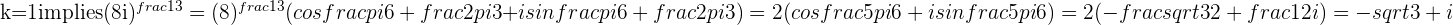
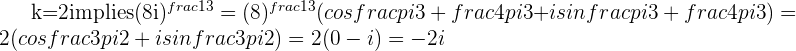
Example
The 4th root of 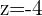
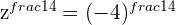
with  and
and 
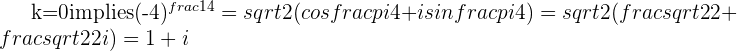
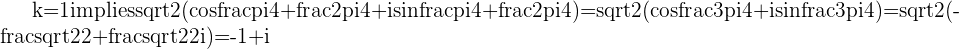
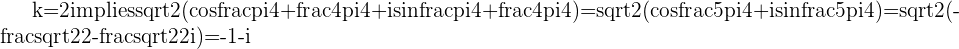
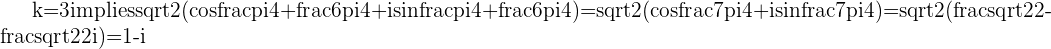
The 5th Roots of -32 in Polar Form

 with
with 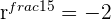 and
and 
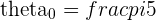

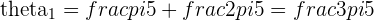
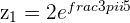

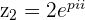
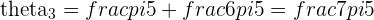

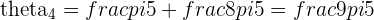
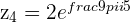
The 8th Roots of Unity
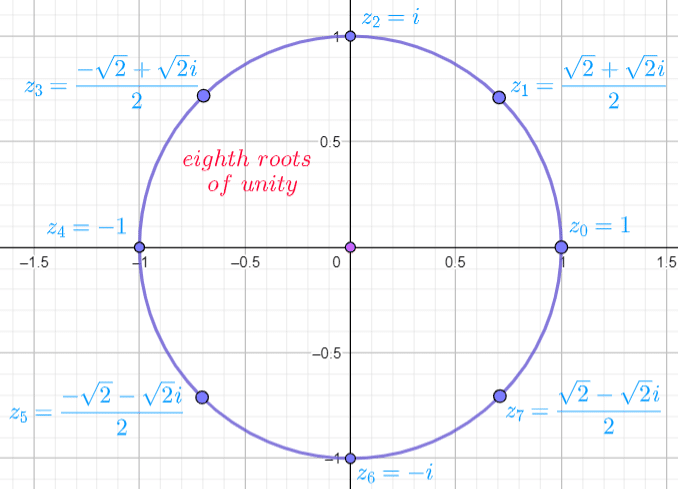
The solutions to the equation  are shown in the picture above:
are shown in the picture above:  .
.
They are all spaced at an angle of 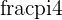 apart as
apart as 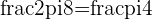 . If there were 6 roots, then the roots would be spread apart by an angle
. If there were 6 roots, then the roots would be spread apart by an angle  .
.
They all lie on the circumference of the Unit Circle a distance of  unit away from the origin.
unit away from the origin.













It is a good for me for giving some help in order to understand very well
this qwestion is necessary
l need support for complex numbers , inverse of quadratic equation, set theory