Chapters

Equal Complex Numbers
Two Complex numbers 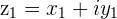 and
and 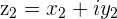 are equal if and only if their Real and their Imaginary parts are equal
are equal if and only if their Real and their Imaginary parts are equal
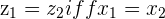 and
and 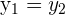
Their arguments are also equal

Example
 with
with 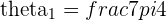 and
and
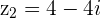 with
with 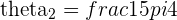
We have equality of the Real and Imaginary parts
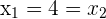 and
and 
and their arguments are also equal
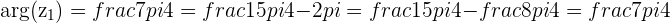
 has traversed an angle larger than
has traversed an angle larger than  but its principle argument is
but its principle argument is  in the 4th Quadrant of the Complex plane.
in the 4th Quadrant of the Complex plane.
Conjugate Complex Numbers
Two Complex numbers 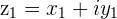 and
and 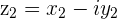 are conjugates if they have equal Real parts and opposite (negative) Imaginary parts
are conjugates if they have equal Real parts and opposite (negative) Imaginary parts
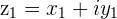 and
and 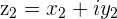 with
with 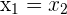 and
and 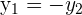
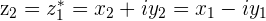 and
and 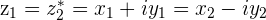
Example
If 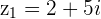 then
then 
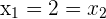 and
and 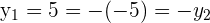
We will denote the conjugate of a Complex number  as
as 

The Modulus of a Complex Number and its Conjugate
The modulus of  is equal to the modulus of
is equal to the modulus of 
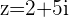 and
and 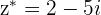
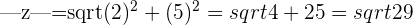 and
and
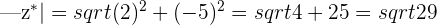
Their product 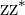 is equal to the square of their modulus
is equal to the square of their modulus
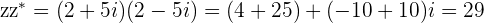 and
and
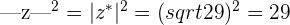
Quadrant Location
We saw from the example above that if a Complex number is located in the 1st Quadrant, then its conjugate is located in the 4th Quadrant. The opposite is also true. If a Complex number is located in the 4th Quadrant, then its conjugate lies in the 1st Quadrant.
The same relationship holds for the 2nd and 3rd Quadrants
Example
If 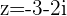 then
then 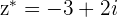
 is located in Quadrant 3, so
is located in Quadrant 3, so  is located in Quadrant 2
is located in Quadrant 2
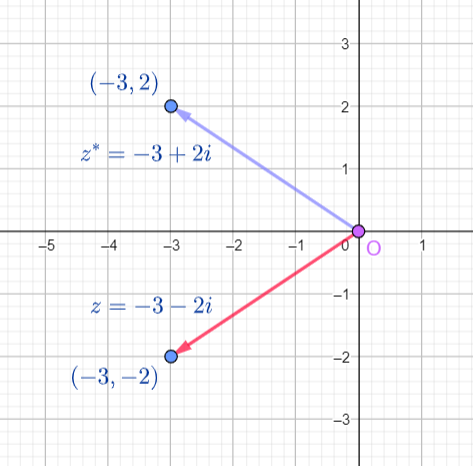
The Argument of a Complex Number and its Conjugate
The arguments of a Complex number  and its conjugate
and its conjugate  add up to
add up to  .
.
If  then
then  because of the symmetry across the
because of the symmetry across the  due to the Quadrant symmetries of 1 and 4 and 2 and 3
due to the Quadrant symmetries of 1 and 4 and 2 and 3
with 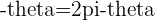
The sum of their arguments is 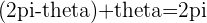 .
.
Opposite Complex Numbers
Two Complex numbers 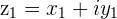 and
and 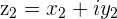 are opposite if they have opposite (negative) Real and Imaginary parts
are opposite if they have opposite (negative) Real and Imaginary parts
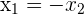 and
and 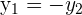 or
or
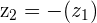
Example
 then its opposite is
then its opposite is 
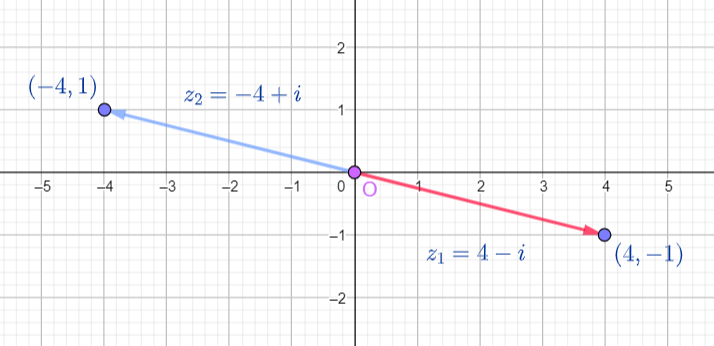
The Modulus of a Complex Number and its Opposite
The modulus of a Complex number  and its opposite
and its opposite  are equal in magnitude
are equal in magnitude
Example
If  then its opposite is
then its opposite is 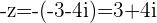
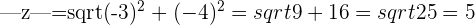 and
and
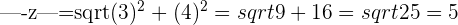
Then  .
.
Quadrant Location
There is also quadrant symmetry between a Complex number and its opposite.
If a Complex number  lies in the 1st Quadrant, then its opposite
lies in the 1st Quadrant, then its opposite  lies in the 3rd Quadrant and if a Complex number
lies in the 3rd Quadrant and if a Complex number 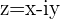 lies in the 4th Quadrant, then its opposite
lies in the 4th Quadrant, then its opposite 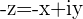 lies in the 2nd Quadrant.
lies in the 2nd Quadrant.
Example
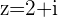 is in the 1st Quadrant because both
is in the 1st Quadrant because both  and
and  are positive, then
are positive, then 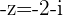 lies in the 3rd Quadrant because both
lies in the 3rd Quadrant because both  and
and  are negative.
are negative.
Example
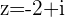 is in the 2nd Quadrant because
is in the 2nd Quadrant because  is negative and
is negative and  is positive, then its opposite
is positive, then its opposite 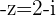 is in the 4th Quadrant because
is in the 4th Quadrant because  is positive and
is positive and  is negative.
is negative.
The Argument of a Complex Number and its Opposite
The arguments of a Complex number  and its opposite
and its opposite  differ by a value of
differ by a value of 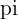 because the numbers lie along a straight line in the plane due to the Quadrant symmetries between 1 and 3 and between 2 and 4, and a straight line has a measure of
because the numbers lie along a straight line in the plane due to the Quadrant symmetries between 1 and 3 and between 2 and 4, and a straight line has a measure of 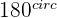 , which is equivalent to
, which is equivalent to 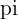 radians.
radians.
Reciprocal Complex Numbers
The reciprocal of a Complex number  is
is  with
with 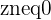 .
.
The reciprocal of a Complex number is its Multiplicative Inverse because 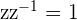 .
.
Example
If  then
then 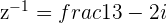
We must rationalize the denominator to make the reciprocal into a form that we can Mathematically manipulate because having a Complex number in the denominator

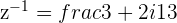 is the conjugate of
is the conjugate of  divided by the square of the modulus. It's just a scaled version of the conjugate of the original Complex number.
divided by the square of the modulus. It's just a scaled version of the conjugate of the original Complex number.
Multiplying a Complex number by its conjugate divided by the square of the modulus will yield  because the product of the Complex number and its conjugate is just the square of the modulus
because the product of the Complex number and its conjugate is just the square of the modulus

Summarise with AI:













It is a good for me for giving some help in order to understand very well
this qwestion is necessary
l need support for complex numbers , inverse of quadratic equation, set theory