Chapters
Like other types of number, composite numbers also holds importance in Maths. The easiest definition of a composite number is a number that has more than two divisors. Yes, composite numbers are the opposite of prime numbers because the condition of the prime number is that it should have only two divisors (which are 1 and itself) while composite number says that it should have more than two divisors. For example, our objective is to find whether the number  is a prime number or composite number? The best way to find whether this is a composite number or not is to divide it by prime numbers which are lesser than
is a prime number or composite number? The best way to find whether this is a composite number or not is to divide it by prime numbers which are lesser than  (because in this example, we are using
(because in this example, we are using  ). If the remainder is a perfect whole number that means a number is a composite number otherwise it will be a prime number. We all know
). If the remainder is a perfect whole number that means a number is a composite number otherwise it will be a prime number. We all know  is a prime number, let's divide
is a prime number, let's divide  by
by  . When we divide
. When we divide  by
by  , the quotient will be
, the quotient will be  and the remainder will be
and the remainder will be  . Although, you can go further on like divide
. Although, you can go further on like divide  by
by  but it is not necessary because the above division is enough to declare that
but it is not necessary because the above division is enough to declare that  is a composite number. Here is another example, find whether
is a composite number. Here is another example, find whether  is a prime or composite number. Now we will divide
is a prime or composite number. Now we will divide  by all the prime numbers below
by all the prime numbers below  .
.
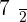 ; remainder =
; remainder =  ,
,
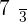 ; remainder =
; remainder =  ,
,
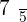 ; remainder =
; remainder =  .
.
Hence, we can conclude that 7 is a prime number, not a composite number. Composite numbers can be expressed as products of powers of prime numbers. Such an expression is called the decomposition of a number in prime factors. For example, decompose  into its prime factors.
into its prime factors.
The first step is to divide the number by 2 (which is the first prime number). Divide the number until the quotient becomes a decimal number. Don't add that decimal number in your division list because that is just an indication.

After that, divide the remaining number by  (because it is the next prime number after
(because it is the next prime number after  ) but when we divide
) but when we divide  by
by  , it doesn't give quotient as a whole number that is why we will jump to the next prime number(which is
, it doesn't give quotient as a whole number that is why we will jump to the next prime number(which is  ):
):

Keep repeat the above step again until you get  :
:
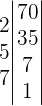
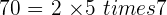
Factoring
To factor a number or to decompose it into factors, carry successive divisions out between its prime divisors.
To make the divisions, use a vertical bar, to the right write the prime divisors and to the left the quotients.

Example
Q. Find the factors of 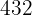 .
.


Find more Maths tuition here on Superprof.
Summarise with AI:













