If you are here that means you know what least common multiple means but that is not all, there is another term known as the greatest common divisor. The easiest definition of the greatest common divisor is the highest number which can divide two or more than two numbers. For example, we have two numbers that are  and
and  , the objective is to find the greatest common divisor of both numbers. When we talk about divisors, there are many divisors of both numbers, let's write it down. The divisors of
, the objective is to find the greatest common divisor of both numbers. When we talk about divisors, there are many divisors of both numbers, let's write it down. The divisors of  are
are  ,
, ,
, , and
, and  , and the divisors of
, and the divisors of  are
are  ,
, ,
, ,
, , and
, and  . If we analyze both divisors then we have some common numbers and they are
. If we analyze both divisors then we have some common numbers and they are  ,
,  ,
,  , and
, and  now the question is which one is the greatest common divisor? Remember the condition for GCD? The number should be the highest and common of the selected numbers. We have gathered all the common divisors now its time to find the highest number. The number
now the question is which one is the greatest common divisor? Remember the condition for GCD? The number should be the highest and common of the selected numbers. We have gathered all the common divisors now its time to find the highest number. The number  is the highest number in that series therefore we can declare
is the highest number in that series therefore we can declare  as the GCD of
as the GCD of  , and
, and  .
.
That was easy, isn't it? But things get complicated when we try to find GCD of big numbers or many numbers. That is why we have a good method that can help you to calculate the greatest common divisor.

Calculation of the Greatest Common Divisor
Below are the steps to find the greatest common divisor.
Step 1
Decompose the number into prime numbers. For example, if you have a number  , break it into its prime factors. The prime factors will be
, break it into its prime factors. The prime factors will be  . This was pretty easy, sometimes it might take you towards long division.
. This was pretty easy, sometimes it might take you towards long division.
Step 2
After the decomposition process, compile the prime numbers. Here is a small tip, if there are more than two same prime numbers then write it into its power form. This will help you in the next step.
Step 3 (Final Step)
Compare and find the common number to find the GCD. For example, you decomposed two numbers into its prime factors and here are the results, 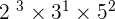 and
and 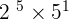 . Now find common numbers with respect to its powers. In the above example, we can get
. Now find common numbers with respect to its powers. In the above example, we can get 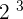 and
and 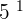 as common, take them out and expand them.
as common, take them out and expand them.



Hence, the GCR for the above example is  .
.
Examples
Determine the GCD of:  ,
, 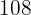 and
and  :
:





 is the largest number that divides
is the largest number that divides  ,
, 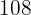 and
and  .
.
If a number is a divisor of another, then this number is the GCD.
The number  is a divisor of
is a divisor of  .
.
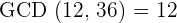
Find more Maths tutor near me here on Superprof.
Summarise with AI:













