Chapters
Mathematicians categorized numbers in different categories such as whole numbers, integers, even numbers, and a few more. One of them is prime numbers. The basic definition of a prime number is a number that has only divisors, one is itself and the other is one. In simple words, if a number that can ONLY be divided by itself AND one is called a prime number. Let's apply this condition on a randomly chosen number. In this example, we will pick the number  , and our objective is to find whether it is a prime number or not.
, and our objective is to find whether it is a prime number or not.
The condition is that  should only be divided by itself and one. This condition isn't fully satisfied because 12 has different factors as well. At this point, you might be thinking that
should only be divided by itself and one. This condition isn't fully satisfied because 12 has different factors as well. At this point, you might be thinking that  can be divided by itself and one but then you need to look at the condition again. If a number that can ONLY be divided by itself AND one is called a prime number and in the case of 12, it can not only be divided by itself and one but there are many other factors such as
can be divided by itself and one but then you need to look at the condition again. If a number that can ONLY be divided by itself AND one is called a prime number and in the case of 12, it can not only be divided by itself and one but there are many other factors such as 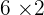 ,
,  ,
, 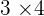 , and
, and 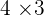 . Hence,
. Hence,  is not a prime number. Let's pick another number, which is
is not a prime number. Let's pick another number, which is  . Apply the condition and think whether
. Apply the condition and think whether  is a prime number or not? If your answer is yes then congratulations! You know what a prime number is. If we look at the factors of
is a prime number or not? If your answer is yes then congratulations! You know what a prime number is. If we look at the factors of  which are
which are 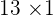 ,
,  . Hence, 13 is a prime number.
. Hence, 13 is a prime number.
We can judge many numbers with the help of this condition but there is one number which creates a lot of conflicts and that is  . The question is whether
. The question is whether  is a prime number or not? The answer is no because we take
is a prime number or not? The answer is no because we take  has only one divisor. The condition speaks of two divisors and in the case of
has only one divisor. The condition speaks of two divisors and in the case of  , there is only one divisor which is
, there is only one divisor which is  and that is why
and that is why  is not a prime number.
is not a prime number.
To find out if a number is prime, orderly divide by prime numbers less than it. When there is no exact division result(meaning remainder is not zero), it is said that the number is prime.
FOR EXAMPLE:
Find if  is a prime number or not?
is a prime number or not?
Numbers below 17 and are prime numbers = 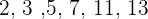

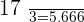


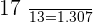
Hence, we can conclude that  is a prime number not a composite number.
is a prime number not a composite number.

ERATOSTHENES SIEVE
The sieve of Eratosthenes is an algorithm that allows one to find all the prime numbers less than a given natural number. This algorithm works by eliminating composite numbers by multiplying each prime number with a series of numbers and eliminating those numbers. The multiplication generates a series of numbers (including that prime number) which has a constant difference.
Find more Maths tutors near me here on Superprof.
How To use Eratosthenes Sieve
Using Eratosthenes Sieve is very easy once you understand it. Below are some key points that will help you to use Eratosthenes Sieve:
- Start with a list of numbers ranging from 2 up to a certain number.
- Eliminate the multiples of 2 from the list.
- Then, take the first number after the 2 that was not eliminated. In this case, (3) and eliminate their multiples from the list, and so on.
- The process ends when the square of the largest number confirmed as a prime number is less than the final number on the list.
- At this point, the numbers that remain on the list are prime numbers.
Example
Calculate this algorithm for all prime numbers less than 40.
1. First, write the numbers. In this case they will be between 2 and 40.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
2. Remove the multiples of 2.
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 15 | 17 | 19 | |||||
| 23 | 25 | 29 | |||||||
| 31 | 35 | 37 |
3. The next number in the list is 3. Since 3² < 40, eliminate the multiples of 3.
| 2 | 3 | 5 | 7 | |||||||
| 11 | 13 | 17 | 19 | |||||||
| 23 | 29 | |||||||||
| 31 | 37 |
4. The next number in the list is 5. Since 5² < 40, eliminate the multiples of 5.
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 29 | ||||||||
| 31 | 37 |
5. The next number in the list is 7. Since 7² > 40, the algorithm ends and the numbers that remain are prime.
| 2 | 3 | 5 | 7 | |||||||
| 11 | 13 | 17 | 19 | |||||||
| 23 | 29 | |||||||||
| 31 | 37 |
Table of prime numbers
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | ||||||||||||
| 23 | 29 | 31 | 37 | ||||||||||||||||
| 41 | 43 | 47 | 53 | 59 | |||||||||||||||
| 61 | 67 | 71 | 73 | 79 | |||||||||||||||
| 83 | 89 | 97 | |||||||||||||||||
| 101 | 103 | 107 | 109 | 113 | |||||||||||||||
| 127 | 131 | 137 | 139 | ||||||||||||||||
| 149 | 151 | 157 | |||||||||||||||||
| 163 | 167 | 173 | 179 | ||||||||||||||||
| 181 | 191 | 193 | 197 | 199 |
Summarise with AI:












