Least common multiple helps a lot in many ways. The basic use of the least common multiple is to find factors of any equation. You must be thinking what is the least common multiple? It is the smallest multiple of two or more than two numbers. This number can't be zero because anything multiplied or divided by zero will always remain zero. This means that every number's LCM will always be equal to zero and that is why we exclude zero.
Let's create some examples for more clarity. For example, you need to find the LCM of  and
and  . The objective is simple, we need to find the smallest common divisor that is common in both
. The objective is simple, we need to find the smallest common divisor that is common in both  and
and  . If we break it into its factor it will be something like this:
. If we break it into its factor it will be something like this:


Now we have the factors as well, we can find the LCM. The condition is that the number should be the smallest number as well as the common number. In the above example, if we multiply 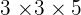 , it will be equal to
, it will be equal to  . Hence, we can declare that
. Hence, we can declare that  is the smallest number that can be divided by
is the smallest number that can be divided by  and
and  . This was pretty simple, right? This is because the numbers were easily broken into its factors but things get complicated as the number increases. That is why we came up with some steps that will help you to tackle any kind of question regarding LCM.
. This was pretty simple, right? This is because the numbers were easily broken into its factors but things get complicated as the number increases. That is why we came up with some steps that will help you to tackle any kind of question regarding LCM.

Calculating the Least Common Multiple
Calculating LCM isn't that hard. In fact, it is very easy once you understand it. Sometimes, you might be given more than  numbers and asked to find the LCM of those numbers. If you don't know how to find LCM then below are the steps to find LCM.
numbers and asked to find the LCM of those numbers. If you don't know how to find LCM then below are the steps to find LCM.
Q. Find the LCM of  ,
, 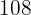 , and
, and  .
.
Step No.1
The first thing is to decompose any number into its prime numbers. In the above example, we can break down the  ,
, 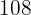 , and
, and  into their prime factors. Here is how you can decompose any number into its prime factors.
into their prime factors. Here is how you can decompose any number into its prime factors.

Step No.2
Once you decompose the numbers into their prime factors, now it's time to arrange them. This arrangement step isn't necessary but this step will make your work easy and a little messy.



Step No.3
This time, you need to take out the highest-powered number of each prime factor. In the above case, we have 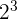 in
in  ,
, 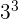 in 108, and
in 108, and  in
in  . Now, multiply these numbers and the resulting number will be LCM.
. Now, multiply these numbers and the resulting number will be LCM.

This concludes that 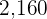 is the smallest number that can be divided by
is the smallest number that can be divided by  ,
, 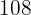 , and
, and  . However, if a number is a multiple of another, then it is the LCM of both. For example, number
. However, if a number is a multiple of another, then it is the LCM of both. For example, number  is a multiple of
is a multiple of  . Hence, we can say that
. Hence, we can say that  is the LCM of
is the LCM of  .
.
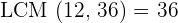
Find more Maths tutor near me here on Superprof.
Relationship between the GCD and LCM
Although GCD and LCM are two different things, however at some points, they can be the same as well. The biggest difference is that the Greatest Common Divisor is the largest integer that can divide two or more than two numbers, on the other hand, Least common multiple is the smallest integer that can divide two or more than two numbers. Yet, you will find that GCD will be equal to LCM so don't get confused, it is normal. That is why we have an example in which you will see that LCM and GCM are same.

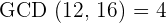
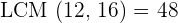


Summarise with AI:













