In order to perform division operation, you need to understand the mechanism of division. When you are dividing two numbers, you have  different things to consider. They are dividend, divisor, quotient, and remainder. We, usually, don't give much importance to the remainder but that doesn't mean it is useless. In this topic, we will discuss the importance of the divisors and its role in the dividing operation.
different things to consider. They are dividend, divisor, quotient, and remainder. We, usually, don't give much importance to the remainder but that doesn't mean it is useless. In this topic, we will discuss the importance of the divisors and its role in the dividing operation.
Divisors are the number that divides any number you want. For example, we want to divide  into equal parts. To do that, we can use
into equal parts. To do that, we can use  as a divisor which will divide
as a divisor which will divide  into
into  equal parts leaving nothing behind. In short, divisors are numbers that help in dividing a dividend. At this point, you might be wondering whether the remainder should be zero to call the number dividend? No, it is not necessary. Sometimes, dividend fails to divide any number into equal parts and that is normal. For example, if we divide
equal parts leaving nothing behind. In short, divisors are numbers that help in dividing a dividend. At this point, you might be wondering whether the remainder should be zero to call the number dividend? No, it is not necessary. Sometimes, dividend fails to divide any number into equal parts and that is normal. For example, if we divide  by
by  , it won't be an exact division, the answer will be
, it won't be an exact division, the answer will be 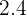 and as you can see, it is not an exact division. This means we are getting a remainder and that is
and as you can see, it is not an exact division. This means we are getting a remainder and that is  . Let's summarize this division, when we tried to break
. Let's summarize this division, when we tried to break  into equal parts, we got
into equal parts, we got  equal parts but there was a small portion that remains unequal. That unequal part is left as a remainder and in order to get all equal parts, we use the decimal method to divide it into equal parts. In conclusion, it is not necessary that the division will always be exact, it can get complicated.
equal parts but there was a small portion that remains unequal. That unequal part is left as a remainder and in order to get all equal parts, we use the decimal method to divide it into equal parts. In conclusion, it is not necessary that the division will always be exact, it can get complicated.
However, if the division is exact then you can call the divisors factors as well. The reason is simple, factors also mean division but the condition is that the division should be an exact division. If the remainder is zero, it means the division is exact and hence we can call the divisor as a factor of dividend. For example, we have a number  , if we divide it by
, if we divide it by  (divisor), we will get a remainder zero. Hence
(divisor), we will get a remainder zero. Hence  is a factor of
is a factor of  . Let's create another example, we picked a new number
. Let's create another example, we picked a new number 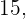 if we divide it by
if we divide it by  , we will again get remainder zero. Therefore,
, we will again get remainder zero. Therefore,  is a factor of
is a factor of  .
.
Find more Maths tutor near me here on Superprof.

Properties of the Divisors
Of course, there are some properties of divisors. These properties define what a divisor is. Below are all the properties.
- A number, other than zero, is a divisor of itself.
- The number one is a divisor of all numbers.
- Any divisor of a number other than zero is smaller than or equal to it, therefore the number of divisors is finite.
- If a number is a divisor of two others, it is also a divisor of their sum and their difference.
- If a number is a divisor of another, it is also a divisor of all the multiples of that number.
- If a number is a divisor of another number, and that number is a divisor of a third one, the first number is also a divisor of the third number.
Prime Factorization
The best way to decompose any number is to break it down into its prime factors. This will not only make your work easy but it will save a lot of your time. To decompose a number into factors, make successive divisions among its prime divisors to obtain one as the quotient. To make the divisions use a vertical bar, to the right write the prime divisors and to the left the quotients.


Number of Divisors
The number of divisors tells you the numbers of divisors of a certain number. For example, we need to find the number of divisors of  . Don't worry, we will tell you how to find the number of divisors, for now, the answer is
. Don't worry, we will tell you how to find the number of divisors, for now, the answer is  . This means that there are
. This means that there are  number of divisors for
number of divisors for  .
.
To obtain the number of divisors, you need to add the unit to the exponents and multiply the obtain results.

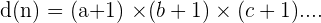
Number of dividers of 
Summarise with AI:













