Chapters
Euclidean Algorithm is very useful when finding the greatest common divisor. Before we start what is the Euclidean Algorithm, you should know what algorithm means. The common understanding is that algorithm is a sequence of steps that solves a problem. Whether it is used for programming or solving a mathematical equation, we use algorithms to get solutions. Many people think the algorithm is only used to give commands to a computer, they are not entirely wrong. You will see that algorithms are mostly used in the computer field but not every time, you will see that we construct a set of rules to solve a problem such as in this article. Yes! you will learn how you can develop a series of rules that will help you to find the highest common divisor.
Euclid's algorithm is a procedure for calculating the greatest common divisor (GCD) of any two numbers. Greatest common divisor (GCD) is the highest positive integer that can divide two or more than two numbers for example, let's take 2 numbers which are 10 and 20. You can get many factors like 2, 5, and 10 but when we will talk about the greatest or highest common divisor than it will be only 10. The reason is simple, GCD means the greatest number which can divide both numbers and in the above example, it can only be 10. At this point, you might be wondering we don't need a huge algorithm to find GCD, we just did it in just a single step in the above example but that was a very simple example, things get complicated when a big number is introduced let's say 232:542? Then you will need Euclid's Algorithm to solve it.

How to use Euclid's Algorithm
The formula of Euclid's algorithm is pretty simple but when it comes to solving a problem then it will become complicated. Below is how you find GCD(A, B) by using the Euclidean Algorithm:
- If A=0 that means GCD(A, B) will be equal to B because A=0 means GCD(0, B) and hence you get the answer B, and then only you can stop the algorithm.
- If B=0 that means GCD(A, B) will be equal to A because B=0 means GCD(A, 0) and hence you get the answer A, and then only you can stop the algorithm.
- You need to write A in the form of quotient remainder (i.e.
 )
) - Find GCD(B, R) using the Euclid's Algorithm since GCD(A,B) = GCD(B, R)
Let's use this algorithm to find the GCD(72,16). These are the steps that you need to follow to obtain GCD.
Find more Maths tutor near me here on Superprof.
Step 1
Divide the largest number by the smallest. In the above example, the largest number is 72 while the smallest number is 16. This means that you need to divide 72 by 16 which will give you 4 and a remainder of 8 but before doing this all, you need to remember something and that is to check the values are either zero or not. In the above example, both 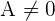 and
and  which indicates that we can use the long division to solve it. Hence,
which indicates that we can use the long division to solve it. Hence,  with remainder
with remainder  . You need to present it in the form of quotient remainder:
. You need to present it in the form of quotient remainder: 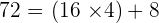 .
.
Since you find that the GCD(72, 16) = GCD(16, 8) but we can't stop here because the only condition to terminate this algorithm is to get either 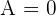 or
or 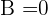 hence we will again divide the largest number (which is 16) with the smallest number (which is 8):
hence we will again divide the largest number (which is 16) with the smallest number (which is 8): 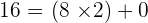 , now we got remainder zero which means
, now we got remainder zero which means 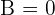 and now we will stop.
and now we will stop.
Step 2
If:
1. The division is exact, the divisor is the GCD.
2. The division is not exact, divide the divisor by the remainder obtained and continue in this process to obtain an exact division. The last divisor is GCD.
GCD (72, 16) = 8
Examples
Q. Find GCD(56, 12) with the help of the Euclidean Algorithm.

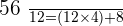
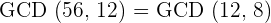

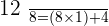
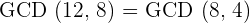

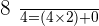

Hence, 
Summarise with AI:













