Chapters

Exercise 1
A beacon flashes its light every  seconds, another every
seconds, another every  seconds, and a third every minute. At 6.30 pm the three flash simultaneously.
seconds, and a third every minute. At 6.30 pm the three flash simultaneously.
Find out the times when the three flash simultaneously again in the next five minutes.
Exercise 2
A businessman goes to Chicago every  days for one day and another businessman every
days for one day and another businessman every  days, also for only one day. Today, both men are in Chicago.
days, also for only one day. Today, both men are in Chicago.
Within how many days will the two businessmen be in Chicago again at the same time?
Exercise 3
What is the smallest number that when divided on separate occasions,  ,
,  ,
,  , and
, and  , gives the remainder of
, gives the remainder of  in every case?
in every case?
Exercise 4
There are  differently sized casks of wine in a cellar whose capacities are:
differently sized casks of wine in a cellar whose capacities are: 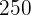 liters,
liters,  liters, and
liters, and 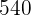 liters. The owner of the cellar wants to package the wine in barrels with an equal amount of wine in each one. Calculate the maximum capacities of these barrels so that the owner can package equal amounts of wine in each cask, and determine the quantity of barrels he will need.
liters. The owner of the cellar wants to package the wine in barrels with an equal amount of wine in each one. Calculate the maximum capacities of these barrels so that the owner can package equal amounts of wine in each cask, and determine the quantity of barrels he will need.
Exercise 5
The floor of a room that needs to be tiled is  m long and
m long and  m wide.
m wide.
Determine the ideal size of the tiles and the number of the tiles needed, such that the number of tiles that are placed is minimal and none of them are to be cut. Keep in mind that all tiles are to be the same size.
Exercise 6
A trader wants to put 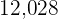 apples and
apples and  oranges into boxes. Each box is to contains an equal number of apples and an equal number of oranges and also the greatest number of each. Find the ideal number of oranges and apples for each box and the number of boxes needed.
oranges into boxes. Each box is to contains an equal number of apples and an equal number of oranges and also the greatest number of each. Find the ideal number of oranges and apples for each box and the number of boxes needed.
Exercise 7
What is the size of the largest possible square tile that can fit an in a room  m long and
m long and 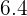 meters wide without being cut? How many tiles are needed?
meters wide without being cut? How many tiles are needed?
Find more Maths tutors near me here on Superprof.
Solution of exercise 1
A beacon flashes its light every  seconds, another every
seconds, another every  seconds, and a third every minute. At 6.30 pm the three flash simultaneously.
seconds, and a third every minute. At 6.30 pm the three flash simultaneously.
Find out the times when the three flash simultaneously again in the next five minutes.


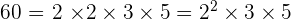


Solution of exercise 2
A businessman goes to Chicago every  days for one day and another businessman every
days for one day and another businessman every  days, also for only one day. Today, both men are in Chicago.
days, also for only one day. Today, both men are in Chicago.
Within how many days will the two businessmen be in Chicago again at the same time?
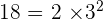

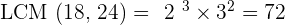
Within 72 days.
Solution of exercise 3
What is the smallest number that when divided on separate occasions,  ,
,  ,
,  , and
, and  , gives the remainder of
, gives the remainder of  in every case?
in every case?
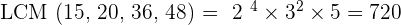
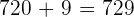
Solution of exercise 4
There are  differently sized casks of wine in a cellar whose capacities are:
differently sized casks of wine in a cellar whose capacities are: 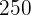 liters,
liters,  liters, and
liters, and 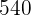 liters. The owner of the cellar wants to package the wine in barrels with an equal amount of wine in each one. Calculate the maximum capacities of these barrels so that the owner can package equal amounts of wine in each cask, and determine the quantity of barrels he will need.
liters. The owner of the cellar wants to package the wine in barrels with an equal amount of wine in each one. Calculate the maximum capacities of these barrels so that the owner can package equal amounts of wine in each cask, and determine the quantity of barrels he will need.
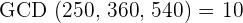
The capacity of the barrels=  liters
liters
Number of barrels of C1 = 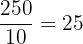
Number of barrels of C2 = 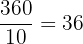
Number of barrels of C3 = 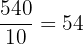
Number of barrels = 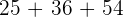 =
=  barrels.
barrels.
Solution of exercise 5
The floor of a room that needs to be tiled is  m long and
m long and  m wide.
m wide.
Determine the ideal size of the tiles and the number of the tiles needed, such that the number of tiles that are placed is minimal and none of them are to be cut. Keep in mind that all tiles are to be the same size.


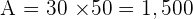 dm²
dm²
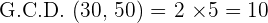 dm aside
dm aside
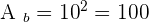 dm 2
dm 2
 dm² :
dm² :  dm² =
dm² =  tiles
tiles
Solution of exercise 6
A trader wants to put 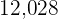 apples and
apples and  oranges into boxes. Each box is to contains an equal number of apples and an equal number of oranges and also the greatest number of each. Find the ideal number of oranges and apples for each box and the number of boxes needed.
oranges into boxes. Each box is to contains an equal number of apples and an equal number of oranges and also the greatest number of each. Find the ideal number of oranges and apples for each box and the number of boxes needed.
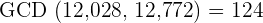
 oranges in each box.
oranges in each box.
Boxes of oranges = 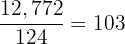
Boxes of apples = 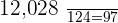 12,028/124 = 97
12,028/124 = 97
Boxes necessary = 
Solution of exercise 7
What is the size of the largest possible square tile that can fit an in a room  m long and
m long and 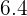 meters wide without being cut? How many tiles are needed?
meters wide without being cut? How many tiles are needed?


 dm aside
dm aside
 dm²
dm²
 dm²
dm²
 dm² :
dm² :  dm² =
dm² =  tiles
tiles
Summarise with AI:













