Chapters
In this article, we will discuss the properties of exponents. We will also solve some examples using these properties. But before proceeding to the properties of exponents, first, let us define power.

What is Power?
Power of a number or a variable refers to the repeated multiplication of that number or variable by itself
Power is also known as an exponent and it is a shorter way of expressing the repeated multiplication of the number by itself. For instance, the expression 3 x 3 x 3 x 3 x 3 can be written in power form as 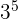 because 3 is multiplied by itself 5 times.
because 3 is multiplied by itself 5 times.
Properties of Exponents
Some of the properties of exponents are given below.
Product Rule
The exponent product rule says that when two expressions with the same bases but different powers are multiplied with each other, we keep the base the same and add their powers.
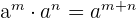
Quotient Rule
The exponent quotient rule says that when the expression with the same bases but different powers are divided by each other, then we keep the base the same and subtract their powers.
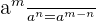
Power Rule
According to the exponent power rule, when power is raised to the power, we multiply the powers together. For instance, consider the following expression:
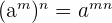
Negative Exponent
The negative exponent rule says that the negative exponent in the numerator becomes positive when we move it to the denominator, and the negative exponent in the denominator becomes positive when we move it to the numerator. For instance, consider the following expressions with negative exponents:


Zero Rule
The exponent zero rule says that any non-negative number raised to the power zero is equal to 1. For example, consider the following expressions with zero exponents:

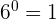
Minus one Rule
The minus one rule of the exponents says that if the power of -1 is an even number, then the result of the expression is 1. On the other hand, if the power of -1 is an odd number, then the result is equal to -1. Consider the following expressions with even and odd exponents:
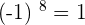
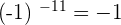
Fractional Exponent
Consider a number m with fractional exponent 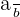 . It can be written as:
. It can be written as:

In the next section, we will solve some examples in which we will solve the expressions using the exponent rules.
Example 1
Solve 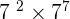
Solution
The above expression has same base 7 but different exponents. We will employ the exponent product rule here which says that when two exponents with the same base are multiplied, we can add their exponents.
= 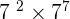
= 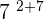
= 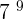
Example 2
Solve 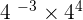
Solution
The above expression has same base 4 but different exponents. Before using the exponent product rule, we will first make the exponent negative exponent positive by shifting it to the denominator like this:
= 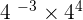
= 
= 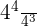
Now, we will further simplify the expression by using the exponent quotient rule which says that when same bases with different powers are divided by each other, we keep the base the same and subtract the powers:
= 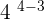
= 
Example 3
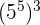
Solution

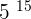
Example 4
Solve 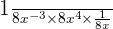
Solution
The above expression has same base 8x but different exponents. Before using exponent product rule, we will first make the exponent negative exponent positive by shifting it to the numerator like this:
= 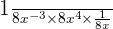
= 
Now, we will use exponent product rule here which says that when two exponents with the same base are multiplied, we can add their exponents.
= 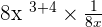
= 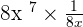
= 
Now, we will further simplify the expression by using the exponent quotient rule which says that when same bases with different powers are divided by each other, we keep the base the same and subtract the powers:
= 
= 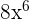
Example 5
Solve 
Solution
Here, we will use exponent quotient rule which says that hen same bases with different powers are divided by each other, we keep the base the same and subtract the powers:
= 
= 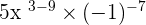
= 
 is equal to -1 because when -1 is raised to an odd power, then it is equal to -1.
is equal to -1 because when -1 is raised to an odd power, then it is equal to -1.
= 
= 
This expression can be simplified further because we can make the negative exponent positive by moving it to the denominator:
= 
Example 6
Solve 
Solution
Here, we will use exponent quotient rule which says that hen same bases with different powers are divided by each other, we keep the base the same and subtract the powers:
= 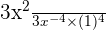
= 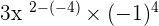
= 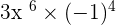
 is equal to 1 because when -1 is raised to an even power, then it is equal to 1.
is equal to 1 because when -1 is raised to an even power, then it is equal to 1.
= 
= 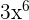
Example 7
Solve 
Solution
The above expression has same base 5x but different exponents. Before using exponent product rule, we will first make the exponent negative exponent positive by shifting it to the numerator like this:
= 
= 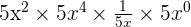
Now, we will use exponent product rule here which says that when two exponents with the same base are multiplied, we can add their exponents.
= 
= 
= 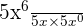
Now, we will further simplify the expression by using the exponent quotient rule which says that when same bases with different powers are divided by each other, we keep the base the same and subtract the powers:
= 
According to the zero exponent rule, a number or coefficient with zero exponent is equal to 1. Hence,  is equal to 1:
is equal to 1:
= 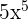
Example 8
Simplify 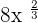
Solution
We will use fractional exponent rule here.
= 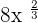
= 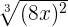
= 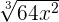
Example 9
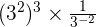
Solution
First, we will make the negative exponent positive by shifting it to the numerator:
= 
Now, we will use exponent power rule which says that when power is raised to the power, they are multiplied together:
= 

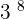
Example 10
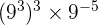
Solution
First, we will make the negative exponent positive by shifting it to the denominator:
= 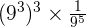
Now, we will use exponent power rule which says that when power is raised to the power, they are multiplied together:
= 
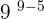

Summarise with AI:












