Chapters

What are Determinants?
The determinant is a scalar value obtained from the elements of the square matrix. In other words, we can say that while computing the determinant, input is a square matrix and output is a scalar number. In a square matrix, the number of rows and columns are equal. The determinant of the matrix is denoted by two vertical lines ||. For example, the determinant of the matrix A will be denoted as |A|.
The determinant of the matrix is an important concept in linear algebra as it is quite helpful in solving linear equations, altering variables in integrals, and telling us how linear transformations alter area or volume. They are also useful in computing the matrix inverse and have some applications in calculus.
The determinant of the 1x1 matrix is the number itself. For example, the determinant of the matrix  .
.
The determinant of the 2x2 matrix is given below:

As we are given the higher order matrices, the calculation of determinants becomes more and more challenging. For example, just look at the following formula for computing the determinant of a 3x3 matrix.

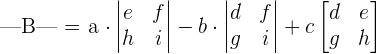
For this matrix, you need to break down the larger matrix into smaller 2x2 matrices. In the next section, we will see how to compute the determinant of the 4x4 matrix.
Calculating the Determinant of a 4x4 Matrix
A 4x4 matrix has 4 rows and 4 columns in it. It would be very time consuming and challenging to find the determinant of 4x4 matrix by using the elements in the first row and breaking the matrix into smaller 3x3 sub-matrices.
In this section, we will see how to compute the determinant of a 4x4 matrix using Gaussian elimination and matrix properties. But before proceeding to examples, you should know what is Gaussian elimination, and different kinds of triangular matrices.
Gaussian Elimination
Gaussian elimination is also called as a row reduction. In linear algebra, the Gaussian algorithm is used to solve the system of linear equations. It is basically a series of operations applied to the matrix elements. This method is helpful in finding the ranks, computing determinants, and inverses of the matrices.
For row reduction, we apply a series of arithmetic operations on the matrix, so that each element below the main diagonal of a matrix becomes zero. This method entails three kinds of row operations:
- Interchanging two rows. The value of the determinant changes its sign, i.e. if it was negative, it becomes positive and vice versa.
- Multiplying a row with a non-zero constant. The determinant remains unchanged.
- Adding or subtracting one row from another. It does not affect the value of the determinant.
Triangular Property of a Matrix
Recall the triangular property of the determinant which says that if each element in the matrix above or below the main diagonal is zero, the determinant is equal to the product of the elements in the diagonal. There are three kinds of triangular matrices:
Upper Triangular Matrix
The matrices in which everything below the diagonal is zero. All non-zero elements are above the main diagonal. For example, consider the following matrix which is in its upper triangular form:
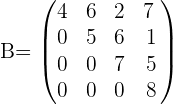
Lower Triangular Matrix
The matrices in which all the elements above the main diagonal are zeroes. All non-zero elements are present below the main diagonal. For example, consider the following matrix which is in the lower triangular form:

Diagonal Matrix
All non zero elements are present on the main diagonal. Everything above or below the main diagonal is zero. For example, consider the following diagonal matrix, where all elements except in the main diagonal are zeroes.

The determinants of such matrices are the product of the elements in their diagonals.
While finding the determinant of a 4x4 matrix, it is appropriate to convert the matrix into a triangular form by applying row operations in the light of the Gaussian elimination method. After we have converted a matrix into a triangular form, we can simply multiply the elements in the diagonal to get the determinant of a matrix.
Example 1
Find the determinant of the following 4x4 matrix.
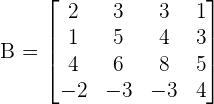
Solution
While finding determinants of the matrices, we can add rows and columns to other rows and columns. It will not affect the determinant of the matrix. Let us apply these operations on the above matrix to convert it into a triangular form:

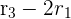

The resultant determinant will look like this:
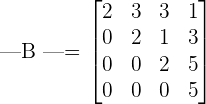
You can see that all elements below the main diagonal are zeroes, therefore this matrix is in the upper triangular form. We will multiply the elements in the diagonal to get the determinant.
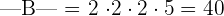
Example 2
Find the determinant of the following 4x4 matrix.
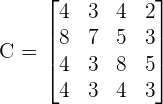
Solution
Let us apply these operations on the above matrix to convert it into a triangular form:

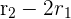

The resultant determinant will look like this:
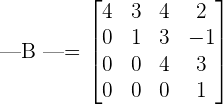
You can see that all elements below the main diagonal are zeroes, therefore this matrix is in the upper triangular form. To get the determinant, we will multiply the elements in the main diagonal.
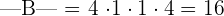
Example 3
Find the determinant of the following 4x4 matrix.

Solution
Let us apply these operations on the above matrix to convert it into a triangular form:

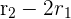

The resultant determinant will look like this:

You can see that all elements below the main diagonal are zeroes, therefore this matrix is in the upper triangular form. You can see below that we have multiplied all the elements in the main diagonal with each other to get the determinant.














Minor of matrix