Chapters

What are Determinants?
Determinants are the values obtained from the elements of a square matrix of order n x n. To compute the determinant, the matrix must be a square one. A square matrix has an equal number of rows and columns. The determinants of the matrices are quite useful in linear algebra as they are employed to solve a system of equations. The determinant of the matrix is denoted by two vertical lines ||. For example, the determinant of the matrix B is represented as |B|.
What are Vandermonde Matrices?
The vandermonde matrix has the terms of geometric progression in each row. In other words, we can say that a Vandermonde determinant presents a geometric sequence in every row or in every column with the first element being 1. The vandermonde determinant is sometimes also known as a discriminant. For example, consider the following vandermonde determinant with the first element of each row equal to 1.
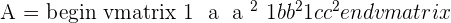
Formula for Computing the Determinant of Vandermonde Matrix
The determinant of a square vandermonde matrix is expressed as follows:
 , where
, where 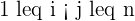
Properties of Determinants
Before proceeding to solve the vandermonde determinants through examples, let us first see some of the properties of determinants:
- The determinant of an identity matrix is equal to 1.
- The determinant of a diagonal matrix is equal to the product of its elements present in the diagonal.
- The determinant of an upper and lower triangular matrix is equal to the product of its diagonal elements.
- A determinant of the matrix is equal to the determinant of its transpose.
- If in a matrix, we multiply one column by a scalar number, then the determinant of such matrix will be also multiplied by that scalar number.
- Adding a constant to a column or a row does not affect the determinant of the matrix.
- If we swap two rows and columns of the matrix, then we will get the determinant with an opposite sign.
- If a matrix has two proportional rows or columns, then the determinant of the matrix will be zero.
Example 1
Find the determinant of the following vandermonde matrix:
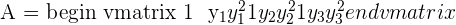
Solution
This matrix is of the order 3x3. Each next term in the row is a geometric progression of the last term. We will solve this example using properties of determinants:
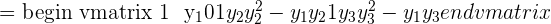

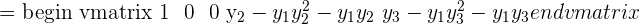
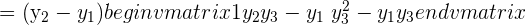
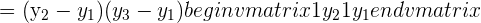
We will use the formula for computing the determinant of a 2x2 matrix here:
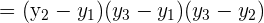
Example 2
Solve the following vandermonde matrix:

Solution
Apply the following row operations to the matrix:
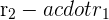
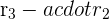

After applying the above operations, we will get the following matrix:

We will eliminate the first row because all the elements are equal to 1. Similarly, after eliminating the first row, we will get a 3 x 4 matrix, in which all elements in the first columns are zeroes. We will eliminate this column as well. The resultant matrix, we will get is of the order 3x3.

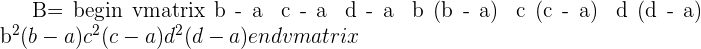
Now, you will notice that the terms (b - a) (c - a) and (d - a) are the factors of all the elements of the matrix. We will write these terms outside the main determinant like this:
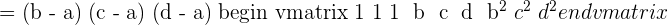
Now , we will apply the following row operations again:

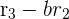
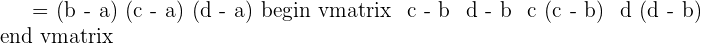
You can see that we have a 2x2 matrix now. Hence, we will simply use the formula for finding the determinant of the 2x2 matrix to solve this example completely.

Example 3
Calculate the determinant of the following vandermonde matrix:

Solution
Apply the following row operations to the matrix:

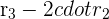
After applying these row operations, we will get the following matrix:
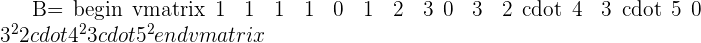
We will eliminate the first row as it has the same number of elements. After eliminating the first row, we will get the matrix with unequal number of rows and columns. The first column will have all zeroes, so we will eliminate that as well.

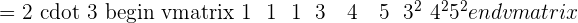
Now, we will apply the following row operations to the above matrix:

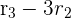
The resultant matrix will be:


Finding Determinant of the Vandermonde Determinant by Formula
We can also employ the following formula to solve the vandermonde determinant.
 , where
, where 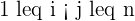
Example 1
This formula may seem tricky, but it is not. We will solve the following vandermonde matrix using this formula.
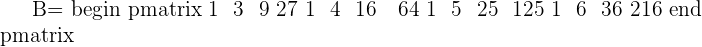
Solution
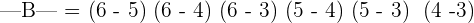

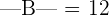
Example 2
Find the determinant of the following vandermonde matrix using the formula.
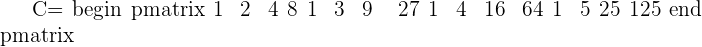
Solution
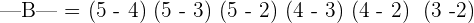

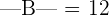













Minor of matrix