Chapters
In this article, we will discuss how to compute the minors and cofactors of the matrices. So, let us first start with the minor of the matrix.

Minor of a Matrix
To find the minor of a matrix, we take the determinant of each smaller matrix, obtained by deleting the corresponding rows and columns of each element in the matrix. Since in the large matrices, there are many rows and columns with multiple elements, therefore we can make many minors of those matrices. We label these minors according to the row and column they belong to.
We know that the square matrix has an equal number of rows and columns in it. It can be of a 2x2 or 3x3 form. Each element in the square matrix has its minor.
For example, consider the following simple square matrix:

To find the minor of each element, we will delete the corresponding row and column of each element and write the minors in the matrix notation.

After writing the matrix in the above form, we will find the determinant of each matrix to compute the minor of the matrix.

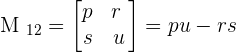

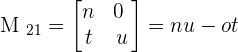

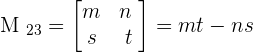
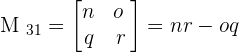
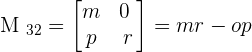
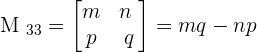
Now, we will solve the following examples to calculate the minor of the matrices.
Example 1
Calculate the minor of the following matrix:

Solution
Write the matrix in the following form. The below matrix is obtained by eliminating the corresponding row and column of each element.

Now, we will compute the determinant of each smaller square matrix. We know that the determinant of the square matrix 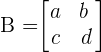 is denoted by
is denoted by  and calculated like this:
and calculated like this:

The resultant matrix will be:
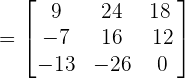
Example 2
Calculate minors of the following matrix:

Solution
Eliminate the corresponding row and column of each element to write the matrix in the following form:
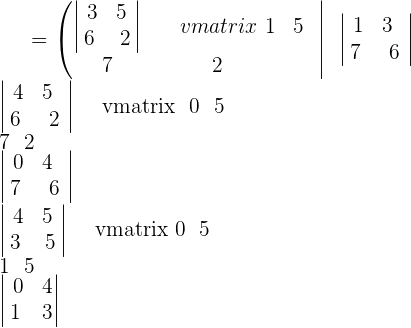
Now, find the determinant of the square smaller matrix to find the minors of all the elements in the matrix:
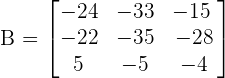
Cofactor
Cofactor of a matrix is related to its minor. Once the minor 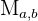 has been computed, we add the two numbers a and b. The number obtained as a result of adding these two numbers is made the value of the power of -1. It is denoted as:
has been computed, we add the two numbers a and b. The number obtained as a result of adding these two numbers is made the value of the power of -1. It is denoted as:

Here, 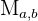 is the minor and
is the minor and 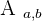 represents the cofactor.
represents the cofactor.
Another simpler way to understand the cofactor of a 3x3 matrix is to consider the following rule.
After finding the minor of the matrix, we change the signs according to this rule to get the cofactor of the matrix:
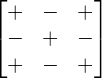
Remember that this rule is for a 3x3 matrix.
We will calculate the cofactors of the matrices in the examples 1 and 2.
Cofactor of Example 1
In example 1, we were given the following matrix:

We found its minors by eliminating the corresponding rows and columns of each element. The resultant minors of the matrix obtained was:
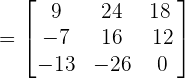
Now, we will apply this rule  to change the sign of each element in the above matrix.
to change the sign of each element in the above matrix.

The above matrix is the cofactor of the matrix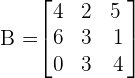 .
.
Cofactor of Example 2
In example 2, we were given the following matrix:

The minors of elements obtained after eliminating the corresponding row and column of each element was below:
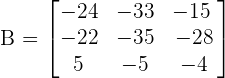
Now, we will apply this rule  . Using this rule to change signs of the elements of the matrix gives cofactors.
. Using this rule to change signs of the elements of the matrix gives cofactors.
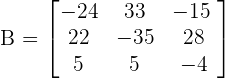
Hence, the above matrix is the cofactor of the matrix.
Relations of Minors and Cofactors with other Matrix Concepts
You may be wondering what is the use of following this cumbersome procedure of finding minors and cofactors of the matrices. Well, these two concepts relate to the other concepts of the matrices. Cofactors and minors are used for computation of the adjoints and inverse of the matrices. The adjoint of the matrix is computed by taking the transpose of the cofactors of the matrix. They also simplify the procedure of finding the determinants of the large matrices, for instance, a matrix of order 4x4.
The Inverse Rule
We use the following rule to calculate the inverse of a matrix using its determinant and cofactors:

Here, 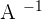 represents the inverse of the matrix
represents the inverse of the matrix
 represents the determinant of a matrix
represents the determinant of a matrix
 represents the matrix of cofactors
represents the matrix of cofactors
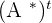 represents the transpose of the cofactor matrix. The transpose of the cofactor matrix is known as adjugate of the matrix.
represents the transpose of the cofactor matrix. The transpose of the cofactor matrix is known as adjugate of the matrix.
This rule says that the inverse of a matrix is equal to the multiplication of the inverse of its determinant by the adjugate of A.













Minor of matrix