Chapters

Exercise 1
Exercise 2
Exercise 3
Exercise 4
Exercise 5
Exercise 6
Exercise 7
Solution of exercise 1
Solution of exercise 2
Solution of exercise 3
Solution of exercise 4
Solution of exercise 5
Solution of exercise 6
Solution of exercise 7

The best Maths tutors available

Exercise 1

Prove, without developing, that the following determinants are zero:

$\text{[math]}$

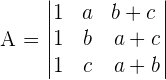
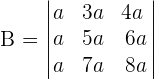
Exercise 2

Knowing that |A|=5, calculate the value of the other determinants.

$\text{[math]}$

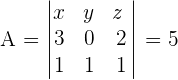
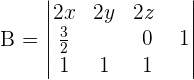
Exercise 3

Prove that the following determinants are a multiple of 5 and 4 respectively, without developing them.

$\text{[math]}$ $\text{[math]}$

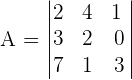
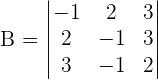
Exercise 4

Prove, without developing, that the following determinant is a multiple of 15:

$\text{[math]}$

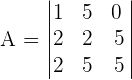
Exercise 5

Prove, without developing.

$\text{[math]}$

Exercise 6

Solve the following equations without developing the determinants.

$\text{[math]}$

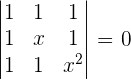
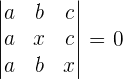
Exercise 7

Prove that the following determinant is divisible by 21:

$\text{[math]}$ ,

Solution of exercise 1

Prove, without developing, that the following determinants are zero:

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

2. $\text{[math]}$

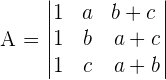
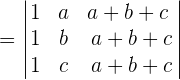
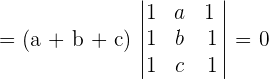
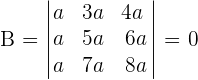
It has two proportional lines. The third column equals the sum of the first two.

Solution of exercise 2

Knowing that |A|=5, calculate the value of the other determinants.

$\text{[math]}$

$\text{[math]}$ $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

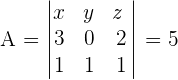
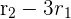
Solution of exercise 3

Prove that the following determinants are a multiple of 5 and 4 respectively, without developing them.

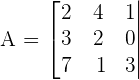
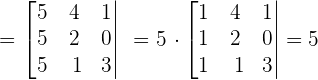
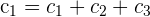
$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Solution of exercise 4

Prove, without developing, that the following determinant is a multiple of 15:

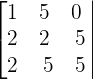
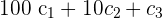
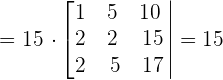
$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Solution of exercise 5

Prove, without developing.

$\text{[math]}$

$\text{[math]}$ $\text{[math]}$

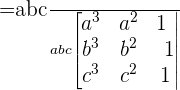
Solution of exercise 6

Solve the following equations without developing the determinants.

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

$\text{[math]}$

$\text{[math]}$ , $\text{[math]}$ and $\text{[math]}$ $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

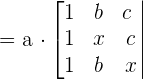
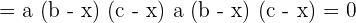
Solution of exercise 7

Prove that the following determinant is divisible by 21:

$\text{[math]}$

$\text{[math]}$ $\text{[math]}$

Did you like this article? Rate it!

4.00 (4 rating(s))

Emma

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.

Determinants Worksheet

Exercise 1

Exercise 2

Exercise 3

Exercise 4

Exercise 5

Exercise 6

Exercise 7

Solution of exercise 1

Solution of exercise 2

Solution of exercise 3

Solution of exercise 4

Solution of exercise 5

Solution of exercise 6

Solution of exercise 7

Determinants

Matrix Rank

4×4 Determinant

Minor and Cofactor

3×3 Determinant

Properties of Determinants

Vandermonde Determinant

Matrix Inverse

Determinant Formulas