Chapters

Introduction to Matrix Rank
The rank of the matrix can be defined in the following two ways:
"Rank of the matrix refers to the highest number of linearly independent columns in a matrix"
OR
"Rank of the matrix refers to the highest number of linearly independent rows in the matrix"
Your result will be equivalent, whether you use the column vectors or the row vectors of the matrix to calculate the rank. Hence, we can say that the number of linearly independent rows or columns represents the rank of a matrix.
A linearly independent row means that it is not the result of the linear combination of the other rows. However, if the row is the linear combination of other rows of the matrix, then it is not termed as a linearly independent row and we can discard it while calculating the rank of the matrix. The same goes with the columns.
Gaussian Elimination Method
- All elements in a row or a column are zero
- A row or column is proportional to the other row or column
- A row or column is a result of the linear combination of other rows and columns
Suppose an m x n matrix has a set of m row vectors and each row has n number of elements. Alternatively, you can say that this matrix has a set of n column vectors, and each column has m number of elements.
Consider an m x n matrix,
- If n is greater than m, then the highest rank of the matrix is m.
- If n is lesser than m, then the highest rank of the matrix is n.
A null matrix is matrix with no elements. You may be wondering what would be the rank of the null matrix. The rank of the null matrix is zero. Similarly, if a matrix has only one element, then its minimum rank will be one.
Calculating the Rank of a Matrix for Determimants
A matrix which has equal number of rows and columns is known as a square matrix. Therefore, if we have a matrix with two rows and two columns, then we say that it is the square matrix of order 2. Similarly, if we have a matrix having three rows and three columns, then we say that it is the matrix of order 3.
In this section, we will see how to find the rank of the matrices using determinants. Before finding the ranks of the matrices using this method, you should know how to find the determinant of a matrix.
- Suppose you have the following 2 x 2 matrix:
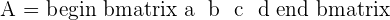
Its determinant will be calculated as follows:
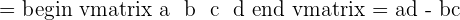
2. Suppose you have the following 3 x 3 matrix.
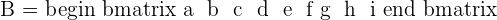
For the computation of its determinant, we will use the following procedure:

It may seem complicated, however once you understand it completely, it becomes straightforward. First you exclude the row and column in which a is present and then multiply it with the determinant of 2 x 2 matrix. The same goes with b and c.
To find the derivatives of the higher order derivatives, it is the best idea to use the matrix calculator because as the order of the matrices increases, the determinant calculation becomes more and more complex.
Now, that you know how to find the determinants of 2 x 2 and 3 x 3 matrices, let us find how to calculate the rank of the matrices using determinants.
Example 1

Solution
Follow these steps to calculate the rank of the matrix.
Step 1
First, we will see if any row or column in the above matrix can be excluded or not. We will look for three conditions to exclude the row or column.
- If all elements are zero. There is no row or column in the matrix B, which has zero elements.
- A row or column is proportional to the other. Again, no row or column in the matrix B is proportional to other.
- A row or column is a linear combination of other rows or columns. Column 3 is a linear combination of column 1 and 2. Therefore, we will exclude it from the rank calculation.
Hence, the resultant matrix will be:

Step 2
In this step, we will check if the rank of the matrix is 1. If there is a non zero square sub-matrix of the order 1, then we say that its rank is 1, because it has a non-zero determinant.
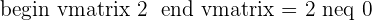
So, yes the matrix has the rank of 1. Now, we will look for the higher order ranks in the next steps.
Step 3
If there is a square sub matrix of order 2 and its determinant is not zero, then we can say that the matrix has the rank of 2.

Yes, the matrix has the rank of 2. We move forward to look for the highest order ranks if and only if the determinant of the square sub matrix is not equal to 0.
Step 4
If we have the square sub matrix of order 3, and its determinant is not zero, then we say that the matrix has the rank of 3.
We have the following three submatrices of the order 3.
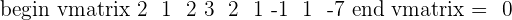
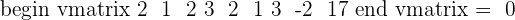

You can see that the determinants of each 3 x 3 sub matrices are equal to zero, which show that the rank of the matrix is not 3.
Hence, the rank of the matrix B = 2, which is the order of the largest square sub-matrix with a non zero determinant.
Example 2
Calculate the rank of the following matrix.

Solution
Follow these steps to calculate the rank of the above matrix.
Step 1
First, we will check, if we can eliminate the rows or columns in the above matrix. You can see that the all the elements in the fourth column are zero. Similarly, the third column is the linear combination of first two columns. Hence we will eliminate these two columns. The resultant matrix will be:
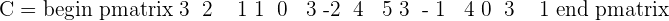
Step 2
Now, we will see that if there is any nonzero square submtarix of order 1. We know that any nonzero element is a square matrix of order 1 whose determinant is not equal to zero. Therefore, we can say that the matrix has the rank of 1. Now, we will look for the higher ranks.
Step 3
Now we will see if there is any non zero square sub matrix of order 2.

Yes, the matrix has the rank of 2. Now, we will look for the higher order rank of the matrix.
Step 4
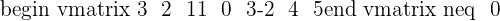

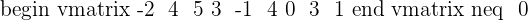
As you can see that the determinants of 3 x 3 sub matrices are not equal to zero, therefore we can say that the matrix has the rank of 3. Since the matrix has 3 columns and 5 rows, therefore we cannot derive 4 x 4 sub matrix from it. It means that we should stop our calculation here, and we will say that the rank of this matrix is 3.













Minor of matrix