Chapters
Determinant of Order One
The matrix of the order one has one element only. The determinant of such a matrix is the element of the matrix itself.


Example
Find the determinant of the matrix  .
.
Solution

Determinant of Order Two
The determinant of the order has two rows and two columns. The formula for finding the determinant of the matrix which is of the order 2x2 is given below:
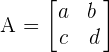

Example
Find the determinant of the following matrix:

Solution

Determinant of Order Three
The matrix of the order three has three rows and three columns. The determinant of such a matrix is given by the following formula:

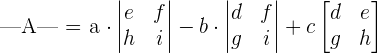
Example
Find the determinant of the following matrix:

Solution
We will put the values from the above matrix in the following formula to compute the determinant.

We will break this matrix into smaller 2x2 matrices, by looking at the first row and multiply each element with the determinant of 2x2 matrix. The 2x2 matrix will be obtained after eliminating the row and column in which the elements 1, 4 and 0 are present,
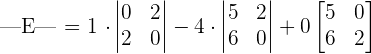
We know that the formula for finding the determinant of the following 2x2 matrix is:


We will employ this formula to calculate the determinants of the smaller 2x2 matrices.
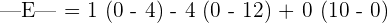


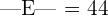
Hence, the determinant of the matrix E is 44.
Rule of Sarrus
It is also known as basketweave method. It is an alternative method of computing the determinant of the 3x3 matrix.
- Elements of the principal diagonal and those of the parallel diagonals with its corresponding opposite vertex have the positive sign.
- The terms with a − sign are formed by the elements of the secondary diagonal and those of the parallel diagonals with its corresponding opposite vertex.

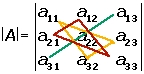
Example
Find the determinant of the following matrix:
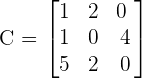
Solution

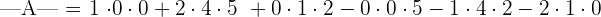














Minor of matrix