Chapters

What are Determinants?
In linear algebra, we can compute the determinants of square matrices. A square matrix is a matrix that has equal number of rows and columns. For example, a square matrix of 2x2 order has two rows and two columns. Similarly, the square matrix of 3x3 order has three rows and three columns. Similarly, we have higher order matrices such as 4x4, 5x5, and so on. Determinants can be employed to analyze or find solutions of linear equations. Besides linear algebra, the determinants have many applications in the fields such as engineering, economics, science and social science.
The determinant of the matrix A is denoted as |A| or det A. It is easy to calculate the determinant of a 2x2 matrix. For example, consider the following square matrix.

The determinant of the above matrix will be denoted as |B|. It is calculated by multiplying the diagonals and placing a negative sign between them.
|B| = mp - no
The determinants of 3x3 and 4x4 matrices are computed using different and somewhat complex procedures than this one. You can also use matrix calculator to calculate the determinants of higher order derivatives.
In this article, we will discuss some of the properties of determinants.
1. Reflection Property
If the rows of the matrix are converted into columns and columns into rows, then the determinant remains unchanged. This property is known as reflection property of determinants. We can also say that the determinant of the matrix and its transpose are equal. To find the transpose of a matrix, we change the rows into columns and columns into rows.
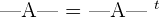
2. All-zero Property
If every element in a row or column is zero, then the determinant of the matrix is zero.
3. Proportionality or Repetition Property
If all the elements of a row or column in a matrix are identical or proportional to the elements of some other row or a column, then the determinant of the matrix is zero.
For example, consider the following matrix in which the second row is proportional to the first row.

Since the elements in the second row are obtained by multiplying the elements in the first row by the number 3, therefore the determinant of the matrix is zero.
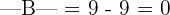
4. Switching Property
If the position of any two rows or columns is interchanged, then the determinant of the matrix changes it sign. It means that if it was positive before interchanging, then it will become negative after the change of position, and vice versa.
For example, consider the following matrix:

The determinant of this matrix is |A| = 18 - 15 = 3
Now, let us see what happens in the rows or columns are interchanged.
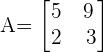
We have interchanged the position of rows. The determinant of the matrix will be |A| = 15 - 18 = -3.
5. Triangle Property
If each element in the matrix above or below the main diagonal is zero, the determinant is equal to the product of the elements in the diagonal.
For example, consider the following matrix:
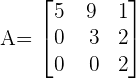
The determinant of the matrix will be:

6. Scalar Multiple Property
If we multiply all the elements of a row or column in the matrix by some non zero constant, then the determinant of such matrix will be multiplied by the same constant.
For example, consider the following matrix:
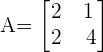
Its determinant is |A| = 8 - 2 = 6
Let us multiply all the elements in the above matrix by 2.

|A| = 16 -4 = 12
You can see in the above example that after multiplying one row by a number 2, the determinant of the new matrix was also multiplied by the same number 2.
7. Sum property
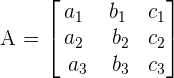
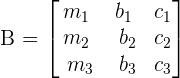
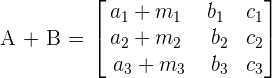
Solve matrices using properties of determinants
Example 1
Apply the properties of determinants and calculate:
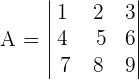
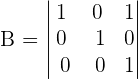
Solution
In this example, we are given two matrices. We need to find the determinants of these matrices. Let us start with the matrix A.
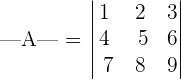
You can see that in the above matrix the rows and columns are proportional to each other. In other words, we can say that when we add 3 to each element in the row 1, we get row 2. Similarly, when we add 3 to each element in the row 2, we get the row 3.
Proportionality or repetition property says that the determinant of such matrix is zero. Hence, we can say that:

Now, let us proceed to the matrix B. In the matrix B, all element above and below the main diagonal are zeros. According to triangular property, the determinant of such a matrix is equal to the product of the elements in the diagonal. Hence,the determinant of the matrix B is:
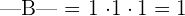
Example 2
Calculate the determinant of the following matrix using the properties of determinants:
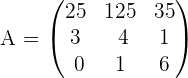
Solution
You can see that in this matrix, all the elements in the first row are multiples of 5. Hence, we can write the first row as:
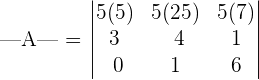
According to the scalar multiple property, the determinant of the matrix will be:


Example 3
Prove that
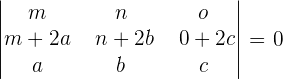
Solution
According to the sum property we can write the determinants as:
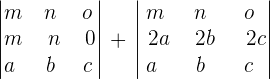
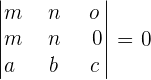
This is because the proportionality property of the matrix says that if all the elements in a row or column are identical to the elements in some other row or column, then the determinant of the matrix is zero.
We can write the determinant of the second matrix by employing the scalar property as:
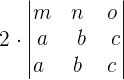
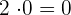
Since the determinants of both the matrices are zeroes, therefore their sum will also be zero.













Minor of matrix