Chapters

What is an Identity Matrix?
To understand the concept of the inverse of a matrix, first, we need to know the concept of an identity matrix. An identity matrix satisfies these three conditions:
- It is always a square matrix, i.e. it should have an equal number of rows and columns
- The diagonal of an identity matrix has the ones. The rest of the elements are the zeros
- We denote the identity matrix by a symbol I
2 x 2 and 3 x 3 identity matrices are given below:
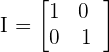
The above matrix is an example of a 2x2 matrix because it has 2 rows and 2 columns.

The above matrix is called 3x3 matrix because it has 3 rows and 3 columns.
You can see that their diagonals have ones and other elements are zeroes.
Now, that you are familiar with the concept of the identity matrix, we will proceed to discuss the inverse of a matrix.
Inverse of a Matrix
For a matrix A, its inverse is 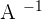 , if and only if it satisfies the following condition:
, if and only if it satisfies the following condition:
 x
x 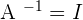
It means that the product of the original matrix and its inverse should be equal to the identity matrix. If this condition is not satisfied, then  is not the inverse of A.
is not the inverse of A.
Now, we will see how to calculate the inverse of the matrix. Consider the following simple matrix of 2 x 2 form. To calculate the inverse of the following 2 x 2 matrix, we will follow the following procedure:

Step 1 - Calculate 
Step 2 - Interchange the positions of a and d.
Step 3 - Reverse the signs of b and c. You will get a new matrix.
Step 4 - Multiply the  with the new matrix to obtain the inverse.
with the new matrix to obtain the inverse.
Let us see some of the examples which will make your concept more clear.
Calculate the inverse of the following matrix.
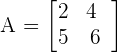
The inverse of the above matrix will be represented as:
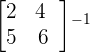
First, we will find  .
.
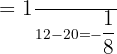
By swapping the positions of 2 and 6 and changing the signs of the numbers 4 and 5, we will get the following new matrix:
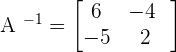
Now, we will multiply 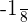 with the above matrix, to get the inverse.
with the above matrix, to get the inverse.
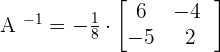

Simplifying the above matrix yields the following inverse of the matrix:
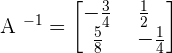
You can check whether the resultant matrix is an inverse of the matrix or not by multiplying it with the original matrix. But to do so, you should be aware of matrix multiplication, i.e. how to multiply two matrices. After the multiplication of the matrix and its inverse, the resultant matrix should be the identity matrix.
Calculating the Matrix Inverse for Determinants
So far, we have discussed how to calculate an inverse of a matrix using a simple procedure. Do you know, how to find the inverse of the matrix using its determinants? Well, in this section, we will see how to use determinants, cofactors and transpose of the matrix to calculate its inverse.
To find the inverse of the matrix using determinants, keep this equation in mind:

Here, 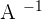 represents the inverse of the matrix
represents the inverse of the matrix
 represents the determinant of a matrix
represents the determinant of a matrix
 represents the matrix of cofactors
represents the matrix of cofactors
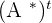 represents the transpose of the cofactor matrix. The transpose of the cofactor matrix is known as adjugate of the matrix.
represents the transpose of the cofactor matrix. The transpose of the cofactor matrix is known as adjugate of the matrix.
Before calculating the inverse of the matrix using its determinants, you should be familiar with how to find the cofactor matrix and its transpose.
How to find cofactor of the matrix?
To find the cofactor of the matrix, you should calculate the minor of each element in the matrix. For example, consider the matrix of the following form:

To find the minors of matrix, delete the row and column in which the element is present.
The minor of the element 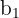 is the following matrix:
is the following matrix:
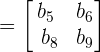
Since we delete the row and column of each element to get the new matrix, so the resultant matrix looks like this:

After writing the matrix in this form, we find the determinant of each smaller matrix. Hence, in this way, we get a whole new matrix which is the minor of the matrix. To find the cofactor of the matrix, we change the sign of each element using this rule:
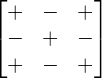
The resultant matrix after changing the signs, is the cofactor of matrix.
How to find the transpose of a matrix?
To find the transpose of the matrix, we switch the rows and columns of the matrix, to get the another matrix. For example, consider the matrix below:
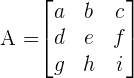
The transpose of the matrix A is represented by  and can be computed by switching the rows and columns:
and can be computed by switching the rows and columns:
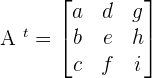
Example 1
Calculate the inverse of the following matrix.
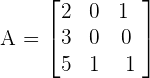
Follow these steps to calculate the inverse of the above matrix using determinants.
Step 1 - Calculate the determinant of the matrix.
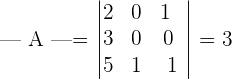
To calculate the determinants of the higher order matrix like the above 3 x 3 matrix, you can use the determinant calculator.
Step 2 - Find the cofactor matrix.

Now, we will find the determinant of each minor to get the following matrix.
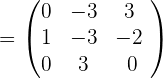
Step 3 - Calculate the transpose of the cofactor matrix.
The transpose of the cofactor matrix is known as adjugate of the matrix
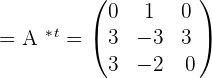
Step 4 - Multiply the matrix with the inverse or reciprocal of the determinant
The matrix inverse is equal to the inverse value of its determinant multiplied by the transpose of the cofactor matrix. In other words, we can say that dividing the determinant with the transpose of cofactor matrix, will yield the inverse.
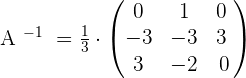
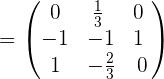
Example 2
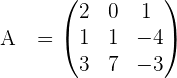
Step 1 - Calculate the determinant of the matrix.

Step 2 - Calculate cofactor of the matrix by finding the minor of each element

Step 3 - Calculate the transpose of the cofactor of matrix.
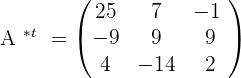
Step 4 - Multiply inverse of the determinant with the cofactor matrix

Now, we will simplify each element in the above matrix, to get the following inverse of the matrix:
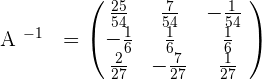













Minor of matrix