Solving Systems of Equations by the Elimination Method

1
Prepare the two equations and multiply by the appropriate numbers in order to eliminate one of the unknown values.
2
Add the systems and eliminate one of the unknowns.
3
Solve the resulting equation.
4
Substitute the value obtained into one of the initial equations and then solve.
5
The two values obtained are the solution of the system.
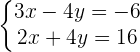
The easiest method is to remove the y, this way the equations do not have to be prepared. However, by choosing to remove the x, the process can be seen better.

Add and solve the equation:
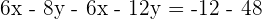


Replace the value of y in any of the equations, we are replacing in the second equation.


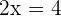

Solution:

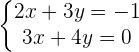
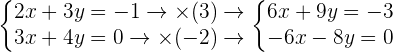
Adding both equations:


Replacing the value of y in the first equation:



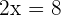

Solution:

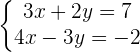
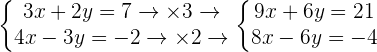
Adding both equations
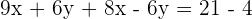


Replacing the value of x in the first equation:
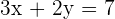



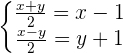

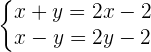
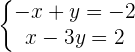
Adding both equations:

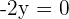

Plugging the value of y in the first equation:
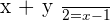

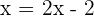
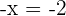

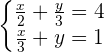

Adding both equations:



Replacing the value of y in the third equation:
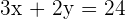

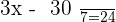
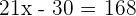
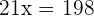

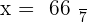
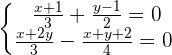



Adding both equations:
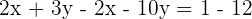

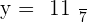
Replacing the value of y in the third equation:

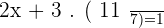



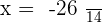

Summarise with AI:













Hi , I m Abhishek Mittal , a passionate maths assistant professor, having experience more than 10 years with almost all top brands (Cuemath, Byjus, FIITJEE, Allen) online and offline and in-person .
Want to join Superprof , Kindly guide me.
Hi Abhishek, thanks so much for reaching out! With your experience, you’d be a fantastic fit for Superprof.
Joining is simple:
1. Visit the Superprof website and click “Become a tutor”.
2. Create your profile, add your teaching experience, qualifications and subjects.
3. Upload a clear photo and write a friendly, detailed description of your teaching style — this really helps students choose you.
4. Set your rates and availability, and once your profile is validated, students can start contacting you directly.
If you need help setting up or optimising your profile, feel free to write to our customer services team at hello@superprof.com — they’ll be happy to guide you!
nice work
Thank you! 😊 We’re glad you found the worksheet helpful. Keep up the great work with your studies!