Name: Elimination Method Questions: Worksheet And Solutions
Brand: Superprof
SKU: SP-RB-00015126
Rating: 4.03 (60 reviews)

Chapters

Example
Word Problem

A system can contain as many equations as you can input. Furthermore, it can contain different types of equations. For example, one equation can be linear, and the other can be a nonlinear equation. We will call this system a nonlinear system of equations. In easy words, a system of equations is nonlinear when at least one of its equations is not in the first degree. The condition is that one of the system's equations shouldn't be linear. However, it can have many nonlinear equations but if we talk about the lower limit, the system should have at least one nonlinear equation.

$\text{[math]}$

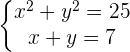
The solution of these systems is usually done by the substitution method. To execute this method, follow the following steps:

1. Work out the value of an unknown in one of the equations, preferably in an equation of the first grade.

$\text{[math]}$

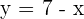
2. Substitute the value of the unknown in the other equation.

$\text{[math]}$

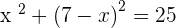
3.Solve the resulting equation.

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

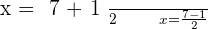
4. Each of the values obtained are substituted into the other equation, and corresponding values of another unknown are obtained.

$\text{[math]}$ $\text{[math]}$

The best Maths tutors available

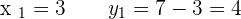
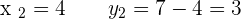
Example

$\text{[math]}$ $\text{[math]}$

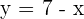
Plugging the value of y in the second equation:

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

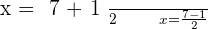
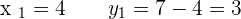
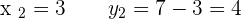
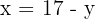
Plugging the above equation in the first equation:

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

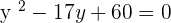
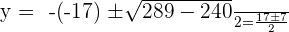
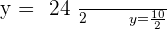
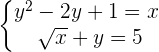
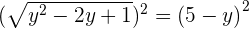
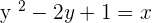
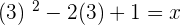
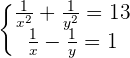
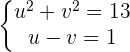
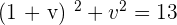
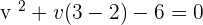
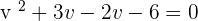
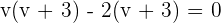
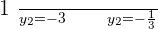
Word Problem

The product of two numbers is 4, and the sum of their squares 17. What are these numbers?

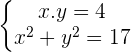
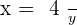
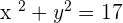
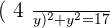
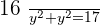
$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Let $\text{[math]}$ :

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

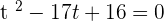
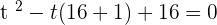
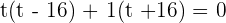
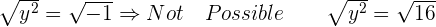
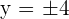
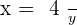
For $\text{[math]}$ :

$\text{[math]}$ $\text{[math]}$

Summarise with AI:

Did you like this article? Rate it!

4.00 (3 rating(s))

Emma

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.

Leave us a comment

Cancel reply

Abhishek Mittal

December 2025

Hi , I m Abhishek Mittal , a passionate maths assistant professor, having experience more than 10 years with almost all top brands (Cuemath, Byjus, FIITJEE, Allen) online and offline and in-person .
Want to join Superprof , Kindly guide me.

Vanessa

December 2025

Hi Abhishek, thanks so much for reaching out! With your experience, you’d be a fantastic fit for Superprof.
Joining is simple:

1. Visit the Superprof website and click “Become a tutor”.
2. Create your profile, add your teaching experience, qualifications and subjects.
3. Upload a clear photo and write a friendly, detailed description of your teaching style — this really helps students choose you.
4. Set your rates and availability, and once your profile is validated, students can start contacting you directly.

If you need help setting up or optimising your profile, feel free to write to our customer services team at hello@superprof.com — they’ll be happy to guide you!

joshua muwanguzi

November 2025

nice work

Vanessa

November 2025

Thank you! 😊 We’re glad you found the worksheet helpful. Keep up the great work with your studies!

Summarise with AI:

Nonlinear Systems of Equations

Example

Word Problem

System of Equations

Elimination Method

Graphing Systems of Equations

Substitution Method