Chapters
Gaussian Elimination Method is another method to find the solution of a system. It is performed on an augmented matrix and we use row operations to find the solution of a specific system. The system should contain linear equations otherwise Gaussian Elimination Method will be a waste of time and effort. Another name for this method is "row reduction". There are two stages in this method, one is the forward elimination and the other is the backward substitution.
Both methods are different. Many students think that they are differed by operations but that is not a valid point, they differ by the results. This means they produce different results. The forward elimination focuses on row reduction to transfer the augmented matrix to echelon form. The biggest purpose of forward elimination is to find whether the system has solutions or not? In case, if the system has no solution that means there is no reason to reduce the matrix in the next stage.
However, if the system looks promising, then backward substitution is carried to find the result of the solution. It is also the last step of the Gaussian Elimination method and it will find the result of the matrix.
System of Three Equations with Three Unknowns
The Gaussian method is to use the elimination method so that in every equation there is one unknown less than in the previous equation.
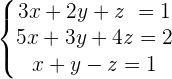
1.Place the equation with the coefficient of x: 1 or −1, as the first equation. If not possible with x, do with y or z, and change the order of the unknowns:

2. Carry out the elimination method with the 1st and 2nd equation to eliminate the term of x in the 2nd equation. Then, in the second equation, place the result of the operation:
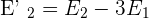
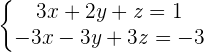
After adding both equations:

3. Do the same with the 1st and 3rd equation to eliminate the term of x:
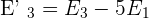

After adding both equations:


4. Perform the elimination method with the 2nd and 3rd equation:
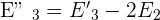
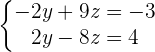
Adding both equations:
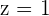
5. Another equivalent system is obtained:

6.Solve the system:
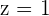
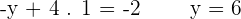


Examples
Q.1


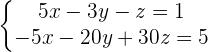
Adding both equations:


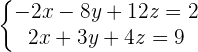
Adding both equations:
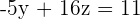
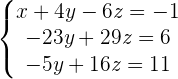
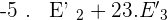

Adding both equations:
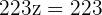
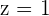

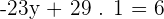



Q.2
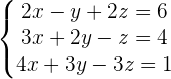

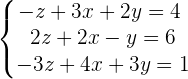
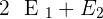
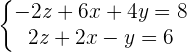
Adding both equations:

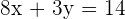


Adding both equations:

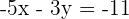
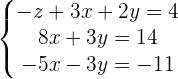


Adding both equation will result:

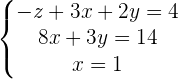
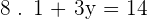

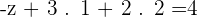
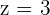
Word Problems
Q.1 A supermarket customer has paid a total of 156 dollars for 24 liters of milk, 6 kg of ham, and 12 liters of olive oil. Calculate the price of each item, knowing that 1 liter of oil costs three times the price of 1 liter of milk and 1 kg of ham costs the same as 4 liters of oil and 4 liters of milk.
milk x
ham y
olive oil z

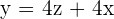
Placing  :
:
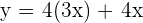

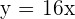





milk 1 dollars
ham 16 dollars
olive oil 3 dollars
Q.2 A video store specializes in films in the following three genres: children, western, and horror. It is known that:
60% of children's movies plus 50% of the westerns account for 30% of all movies.
20% of the children, 60% of the westerns, and 60% of the horror films account for half of all films in the video store.
There are 100 more western movies than children movies.
Find the number of films in each genre.
children x
western y
horror z
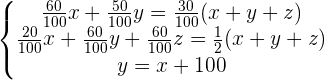
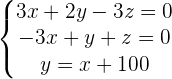
Placing equation 3 in the both equations:
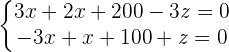
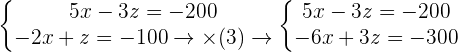
Adding both equations:
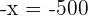
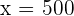
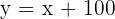



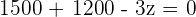
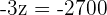
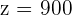
children 500 movies
western 600 movies
horror 900 movies
Q.3 The sides of a triangle are 26, 28, and 34 cm. Centered at each vertex are three circles, tangent to each other. Calculate the length of each circle's radius.

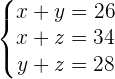




Summarise with AI:













Hi , I m Abhishek Mittal , a passionate maths assistant professor, having experience more than 10 years with almost all top brands (Cuemath, Byjus, FIITJEE, Allen) online and offline and in-person .
Want to join Superprof , Kindly guide me.
Hi Abhishek, thanks so much for reaching out! With your experience, you’d be a fantastic fit for Superprof.
Joining is simple:
1. Visit the Superprof website and click “Become a tutor”.
2. Create your profile, add your teaching experience, qualifications and subjects.
3. Upload a clear photo and write a friendly, detailed description of your teaching style — this really helps students choose you.
4. Set your rates and availability, and once your profile is validated, students can start contacting you directly.
If you need help setting up or optimising your profile, feel free to write to our customer services team at hello@superprof.com — they’ll be happy to guide you!
nice work
Thank you! 😊 We’re glad you found the worksheet helpful. Keep up the great work with your studies!