Chapters
Every equation is different from another. Just changing a single variable, sign, or constant will always result in a new equation. You can say both equations are similar to some extent but, in reality, they are different. The question is how can we prove that a small change can change the whole course? Instead of telling you, we will show how just a small change in an equation can change everything. Imagine that you are in an exam hall and you are asked to find the factors of an equation which is 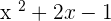 . If you draw a graph of
. If you draw a graph of 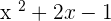 then it would be:
then it would be:
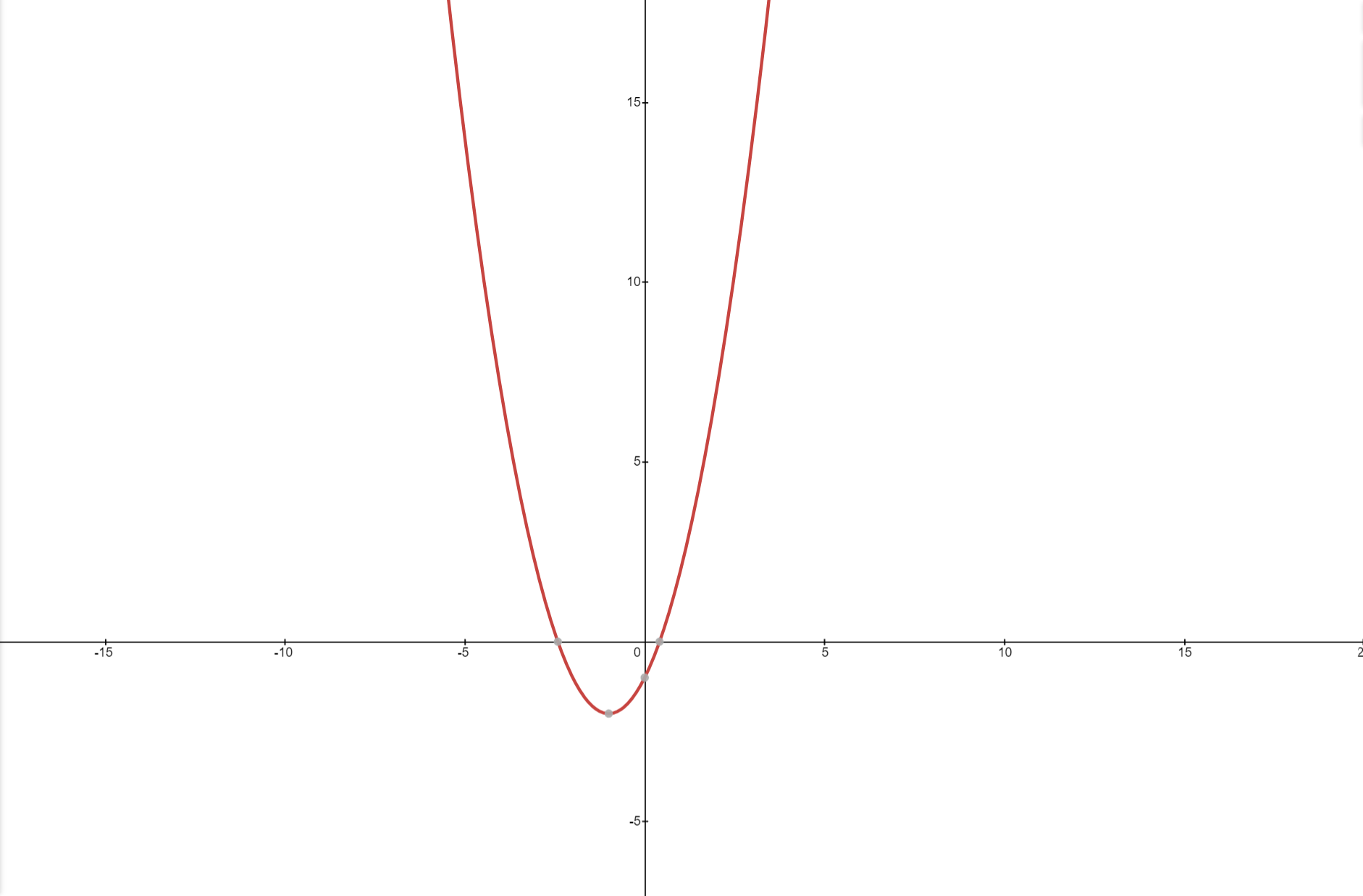
However, you made a tiny mistake of a sign. Instead of 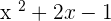 , you wrote
, you wrote 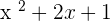 hence, this will change everything. Below is the graph of
hence, this will change everything. Below is the graph of 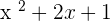 :
:
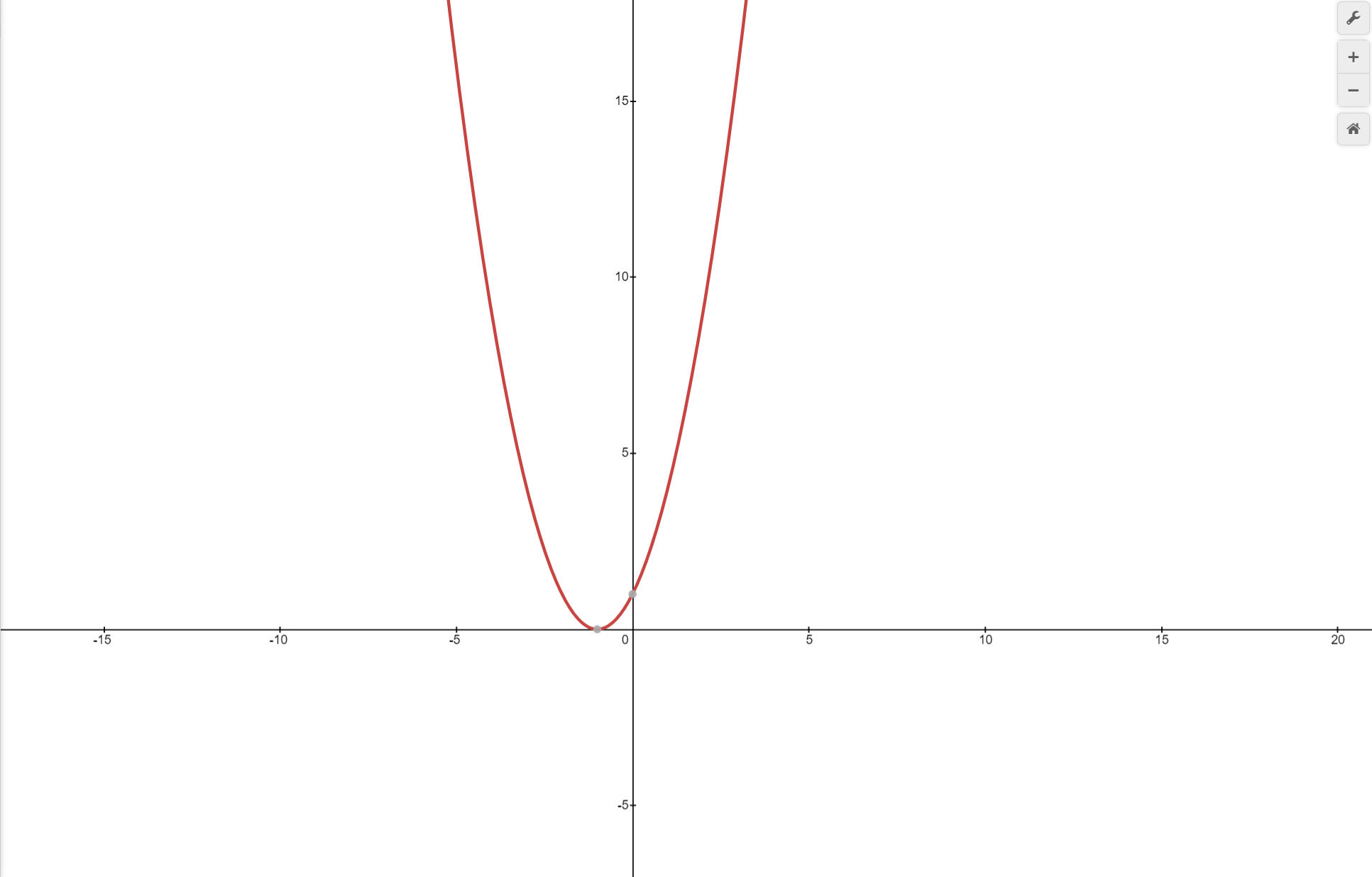
If you look closely, just by changing a single sign, the graph has some changes. We can't ever say that the above graphs are the same but there are similar to some extent. What if tried to draw both graphs on each other?
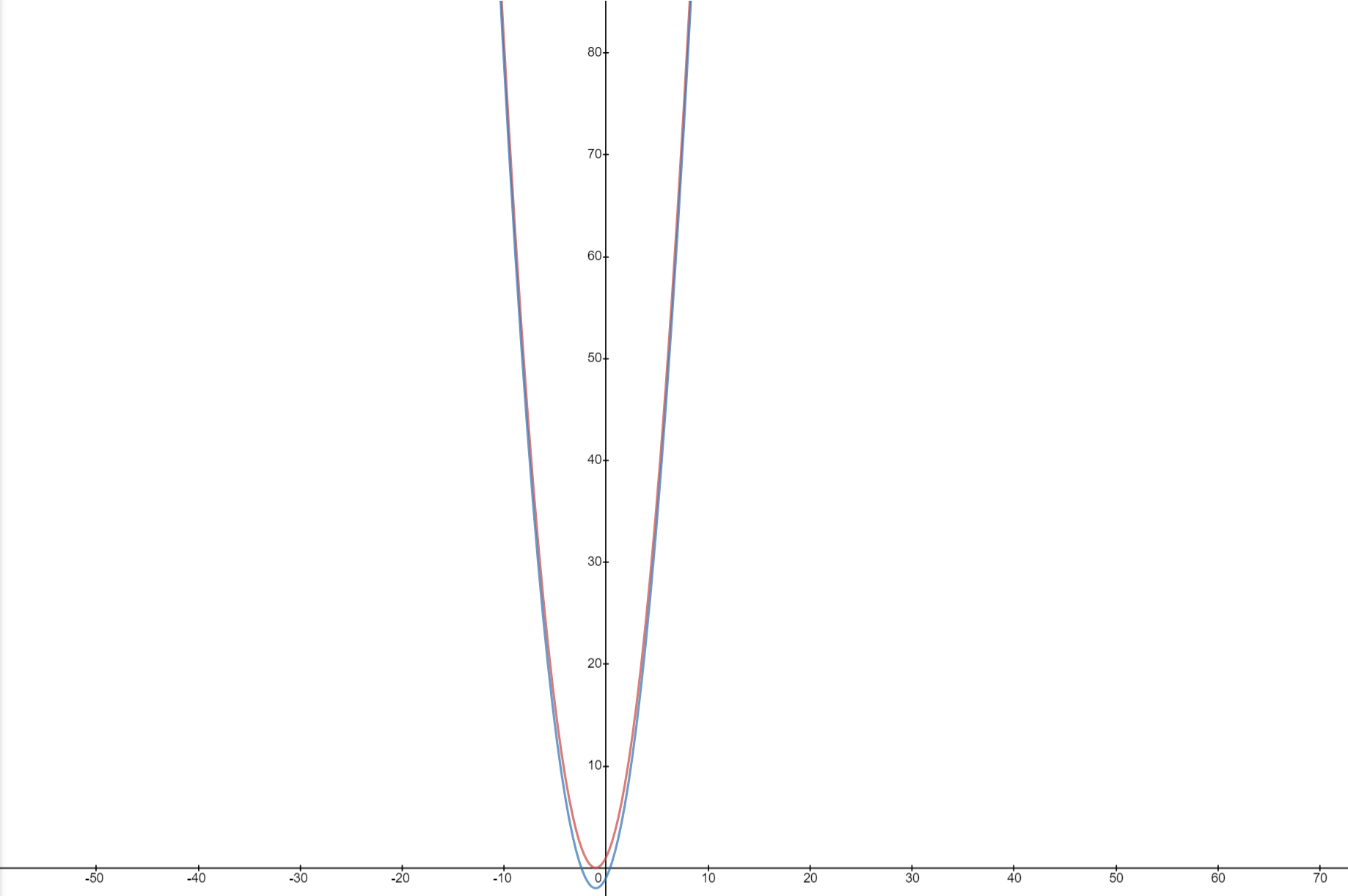
The graph overlaps another graph after some points. We call them intersection points. It means at these points, both graphs intersect each other. Although, this graph contains a lot of intersection points that might be difficult for you to understand and here we make things easy, therefore, below is a graph that has just one intersection point for clarification:
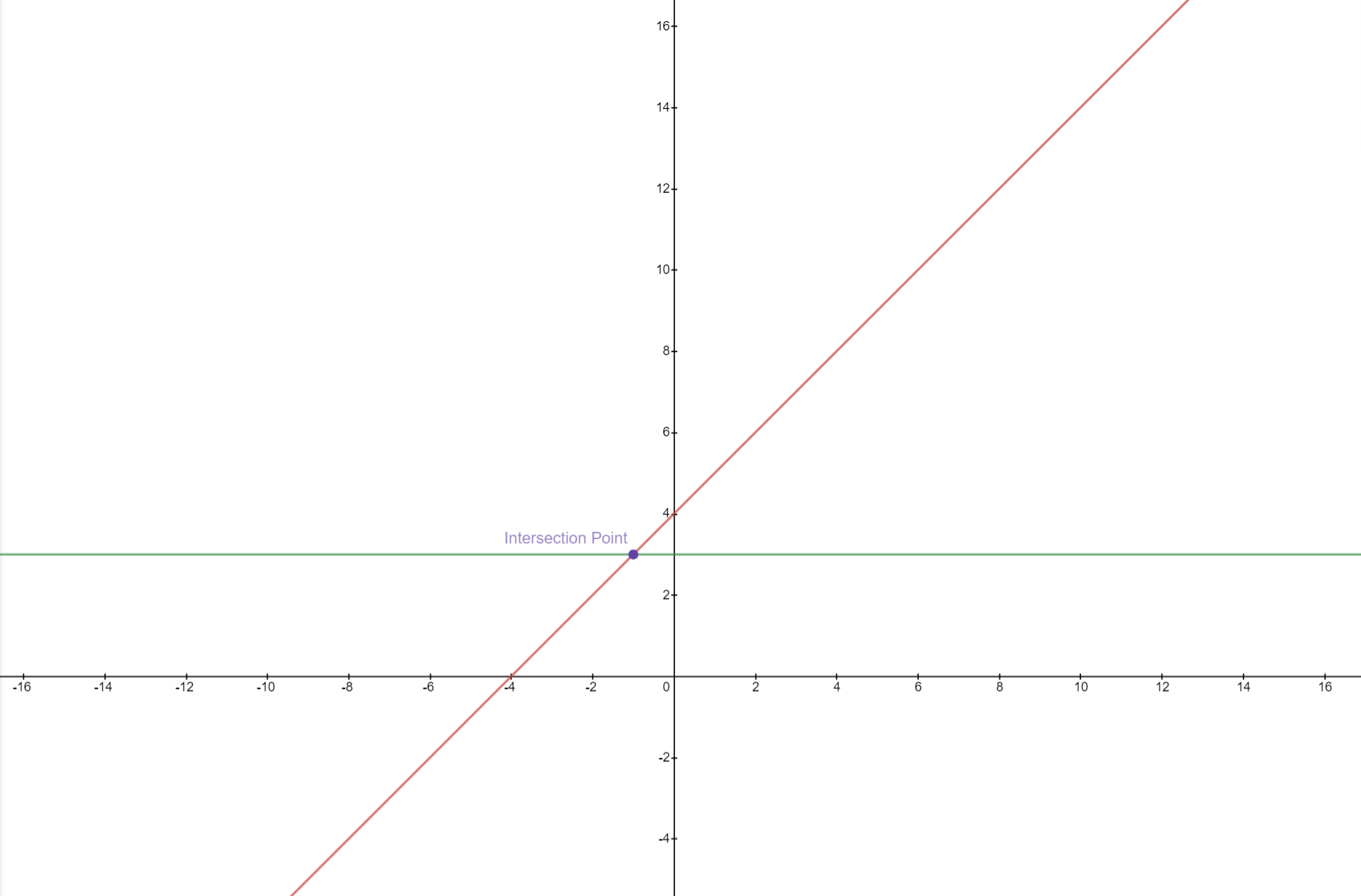
The intersection point is also known as a common solution because if you solve both equations simultaneously, you will get this point. In simple words, two equations with two unknowns form a system if they have a common solution.
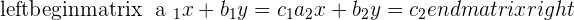
The solution of a system is a pair of numbers x1, y1, such that replacing x with x1 and y with y1, both equations are verified.

Adding both equations:
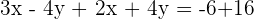
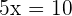

Plugging the value of x in the second equation:

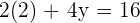

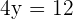


Properties of Linear Systems
1. If both members of an equation in a system are added or subtracted by the same expression, the resulting system is equivalent.
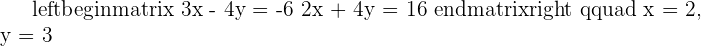
2.If both members of the equations of a system are multiplied or divided by a nonzero number, the resultant system is equivalent.
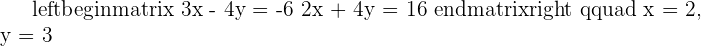
3. If an equation of a system is added or subtracted by another equation of the same system, the resultant system is equivalent.
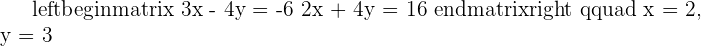
4.If in a system, an equation is replaced by another equation that is obtained from adding the two equations from a system previously multiplied or divided by a nonzero number, the resultant system is equivalent.

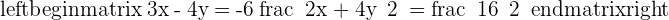
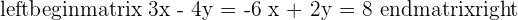


5. If the order of the equations or the order of the unknowns changes, it is another equivalent system.


Summarise with AI:













Hi , I m Abhishek Mittal , a passionate maths assistant professor, having experience more than 10 years with almost all top brands (Cuemath, Byjus, FIITJEE, Allen) online and offline and in-person .
Want to join Superprof , Kindly guide me.
Hi Abhishek, thanks so much for reaching out! With your experience, you’d be a fantastic fit for Superprof.
Joining is simple:
1. Visit the Superprof website and click “Become a tutor”.
2. Create your profile, add your teaching experience, qualifications and subjects.
3. Upload a clear photo and write a friendly, detailed description of your teaching style — this really helps students choose you.
4. Set your rates and availability, and once your profile is validated, students can start contacting you directly.
If you need help setting up or optimising your profile, feel free to write to our customer services team at hello@superprof.com — they’ll be happy to guide you!
nice work
Thank you! 😊 We’re glad you found the worksheet helpful. Keep up the great work with your studies!