Equations vary in many shapes and limits. Every equation is different from another and that is the beauty of equations. One of the most frequently asked questions is that why do we graph a system of equations? The answer is simple, to find solutions of the system. A system can many equations. It means that there is no limit of equations in a system, however, the less they are, the easier they are to solve. Imagine a system with two equations. Both equations are linear and they are plotted on a graph. Finding solutions of that system means that finding all those points at which both lines intersect each other. If your concepts about straight lines are good then you might have predicted that there will be only one set of solution since we are talking about linear equations here but a system can have different types of equations as well. For example, a system has a cubic equation, two straight-line equations, and one quartic equation. This system might have more than one set of solution and in some cases, a system might not have any set of solution and that is why, in this lesson, you will learn types of systems.

Types of Systems
Consistent Independent System
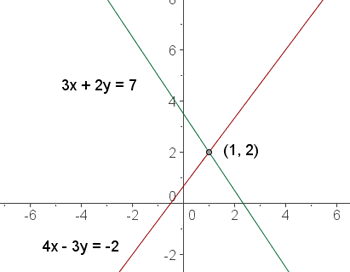
If the system has just one set of solution, that means the system is a consistent independent system.
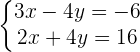
Solution of the system 
Graphically, the solution is the intersection point of the two straight lines.

Consistent Dependent System
If the system has an infinite set of solutions, that means the system is a consistent dependent system.
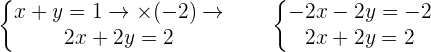
If you solve the above equation, it will result in 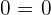 which means that the system will have infinite solutions.
which means that the system will have infinite solutions.
Graphically, two identical straight lines are obtained and any point on the line is a solution.
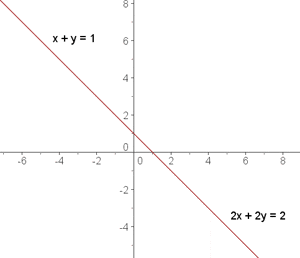
Inconsistent System
If the system has no set of solutions, that means the system is a inconsistent system.
Once you solve both equations simultaneously, you will be left with 
Graphically, two parallel straight lines are obtained.
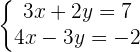
What is the Need For All of This?
You might be thinking what is the benefit of this? This can make your work easier, for example, you are doing research work and found that a system with different equations. You will solve the whole system and let's say you came up with an answer that the system is an inconsistent system. Another researcher carried out your research but in a different location to compare the results. That researcher came up with the same system that you encountered. Now that researcher will waste his/her precious time to solve that equation and not to mention if he/she did a human error then that would lead to numerous results. That is why mathematicians categorized the system. When you published your research work, you will mention the system is an inconsistent system and this will save time for the other researchers, they will need to reference it and this will save a lot of time and effort for other people.
Summarise with AI:













Hi , I m Abhishek Mittal , a passionate maths assistant professor, having experience more than 10 years with almost all top brands (Cuemath, Byjus, FIITJEE, Allen) online and offline and in-person .
Want to join Superprof , Kindly guide me.
Hi Abhishek, thanks so much for reaching out! With your experience, you’d be a fantastic fit for Superprof.
Joining is simple:
1. Visit the Superprof website and click “Become a tutor”.
2. Create your profile, add your teaching experience, qualifications and subjects.
3. Upload a clear photo and write a friendly, detailed description of your teaching style — this really helps students choose you.
4. Set your rates and availability, and once your profile is validated, students can start contacting you directly.
If you need help setting up or optimising your profile, feel free to write to our customer services team at hello@superprof.com — they’ll be happy to guide you!
nice work
Thank you! 😊 We’re glad you found the worksheet helpful. Keep up the great work with your studies!