Chapters
In this article, we will discuss how to compute the areas and volumes of the geometrical figures using vectors. Vector is one of the important concepts in calculus. Before proceeding to specific examples and describing step by step how to do that, first, let us see what are vectors.
Consider the movement of an airplane during a flight. Which two pieces of information are most important to ensure everything is going smoothly? Well, the answer is simple. The direction in which the plane is traveling and its speed are two most important factors. When computing the force, for instance, the thurst of the engine of a plane, it is critical to explain not only the magnitude/strength of that force but also the direction in which that force is applied. Thus, we can say that some quantities are not complete without describing both the magnitude and the direction. The vector is defined as:
The quantity that has a magnitude, as well as direction is known as a vector

Mathematical notation of a vector
A vector is denoted by v with a line segment (an arrow) above it as shown below:
A vector is denoted by  .
.
The endpoints of this line segment are called the initial and terminal points of the vector because the arrow starting from the initial to the terminal point tells us the direction of the vector. The magnitude is determined by the length of the line segment. We can have a vector that has the same initial and terminal points. This vector is known as a zero vector and is denoted by 0. The only vector that has no direction is the zero vector. The equivalent vectors are the vectors with the same magnitude and direction. The equivalent vectors can have different initial points and are represented as:
v = w
Now, we will see how to compute the areas and volumes of the geometrical figures, given the vectors.
Area of Parallelogram
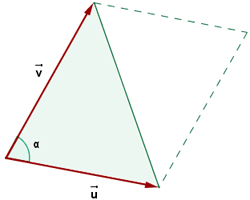
The extent of the cross product of two vectors conforms with the parallelogram area whose sides are those vectors.
Geometrically, the magnitude of the cross product of two vectors coincides with the area of the parallelogram whose sides are those vectors. For example, consider the following figure.
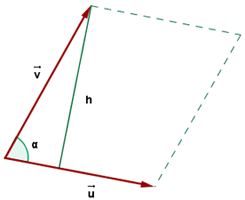
The area of the parallelogram is given below:
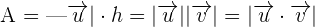
Now, let us solve the following examples.
Example 1
Given the vectors 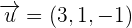 and
and 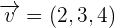 , calculate the area of the parallelogram whose sides are the vectors
, calculate the area of the parallelogram whose sides are the vectors  and
and  .
.
Solution
We will multiply the two vectors to compute the area of the parallelogram.
Area of the parallelogram = 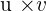
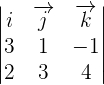
The above determinant is of the form 3x3, i.e., it has 3 rows and 3 columns. We will use the following formula to calculate the determinant of this matrix.
Consider the following 3x3 matrix:

The determinant of the matrix A will be calculated as:
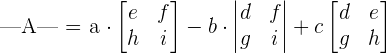
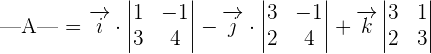


Example 2
Given the vectors 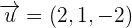 and
and 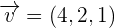 , calculate the area of the parallelogram whose sides are the vectors
, calculate the area of the parallelogram whose sides are the vectors  and
and  .
.
Solution
We will multiply the two vectors to compute the area of the parallelogram.
Area of the parallelogram = 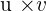

The above determinant is of the form 3x3, i.e., it has 3 rows and 3 columns. We will use the following formula to calculate the determinant of this matrix.
Consider the following 3x3 matrix:

The determinant of the matrix A will be calculated as:
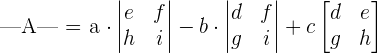

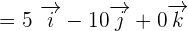
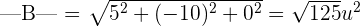
Area of a Triangle
If  is the base of the triangle and
is the base of the triangle and  is its height, then the formula for area of the triangle is:
is its height, then the formula for area of the triangle is:
Area of the triangle = 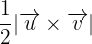
Example
Determine the area of the triangle whose vertices are the points A = (1, 1, 3), B = (2, −1, 5) and C = (−3, 3, 1).
Solution
We will find 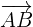 by taking the difference of the coordinates of the vertex B and A.
by taking the difference of the coordinates of the vertex B and A.
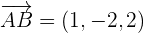
The same process will be repeated for 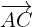 :
:
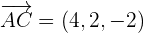
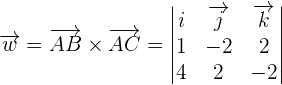
Using the formula for finding the determinant of a 3 x3 matrix, we will calculate the area of the triangle:

The determinant of the matrix B will be calculated as:
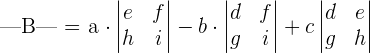
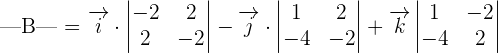
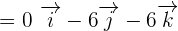
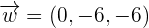

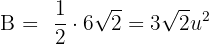
Volume of a Parallelepiped
The absolute value of the triple product depicts the volume of a parallelepiped. The edges of the parallelepiped are three vectors that join the same vertex.
Example
Find the volume of the parallelepiped formed by the following vectors:
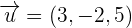


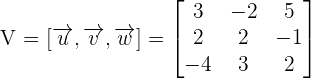
Find the determinant using the following formula:

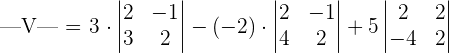
= 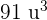
Find various Maths tutors on Superprof.
Volume of a Tetrahedron
The volume of a tetrahedron is equivalent to  of the absolute value of the triple product. Mathematically, we can denote it as:
of the absolute value of the triple product. Mathematically, we can denote it as:
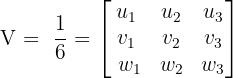
Example
Calculate the volume of the tetrahedron whose vertices are the points A = (3, 2, 1), B = (1, 2, 4), C = (4, 0, 3) and D = (1, 1, 7).
Solution
Calculate the values of 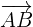 ,
, 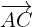 and
and 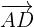 .
.
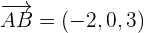

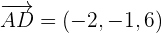
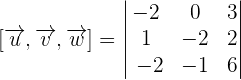
Use the formula of 3x3 determinant to calculate the determinant:
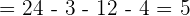
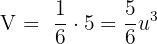













I WANT TO CONTINUE WITH SOLVED PROBLEMS OF APPLICATION OF CROSS PRODUCTS OF VECTORS