Name: Point-Line Distance
Brand: Superprof
SKU: SP-RB-00004725
Rating: 4 (2 reviews)

Chapters

Distance Between Point and the Line
Example 1
Example 2
Example 3
Example 4
Example 5

In this article, we will discuss how to calculate the distance between the point and the line using vectors.

Distance Between Point and the Line

The distance from a point, P, to a line, r, is the shortest distance from the point to one of many points on the line.

The distance is equal to the length of the perpendicular line drawn from the point to the line.

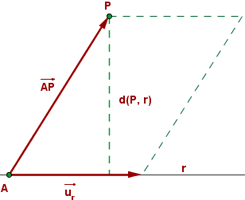
The vector formula to calculate the distance between a line and the point is given below:

$d (P, r) = \frac {|\overrightarrow {u_r} \times \overrightarrow{AP}|} {|\overrightarrow{u_r}|}$

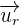Here, $\overrightarrow {u_r}$ represents the direction vectors and 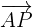$\overrightarrow {AP}$ represents the distance between the point P and point A on the line.

Now, we will see how to calculate the distance between the point and the lines using the above formula.

The best Maths tutors available

Example 1

Determine the distance from the point P = (1, 3, −2) to the line 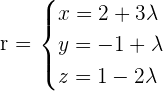$r = \begin{cases} x = 2 + 3\lambda \\ y = -1 + \lambda \\ z = 1 - 2 \lambda \end{cases}$ .

Solution

First, we have to calculate $\overrightarrow{u_r}$ .

We need to treat each of the 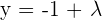$x = 2 + 3\lambda$ , $y = -1 + \lambda$ , and $z = 1 - 2 \lambda$ coefficients on the vector i, j, and k.

$= (2 + 3\lambda) i, (-1 + \lambda)j, ( 1 - 2 \lambda)k$

= $2i + 3\lambda i - 1j + \lambda j + 1k, - 2\lambda k$

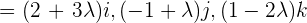
Now, we will make two groups. The first group will have all the values that contain $\lambda$ and the second group will have all he values that don't contain $\lambda$ :

= $2i - j + k + 3\lambda i + \lambda j - 2 \lambda k$

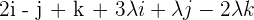
Now, we will factor out 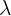$\lambda$ from the second group like this:

= $2i - j + k + \lambda (3i + j - 2k)$

The coefficients in the first group tell us the point from which the line passes through and the coefficients in the second group tell us about the direction vectors.

Hence, the direction numbers for the line are 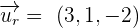$\overrightarrow{u_r} = (3, 1, -2)$ and the coordinates of the point through which the lines passes are $\overrightarrow{A} = (2, -1, 1)$ .

We have to calculate the distance between the point P (1, 3, -2) and point on the line A (2, -1, 1).

Since have both A and P, hence we can easily calculate $\overrightarrow{AP}$ like this:

$\overrightarrow{AP} = (1 - 2, 3 - (-1), -2 - 1) = (-1, 4, 3)$

Now, we will find the cross product of 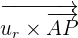$\overrightarrow{u_r \times \overrightarrow{AP}}$ using determinant:

$\overrightarrow{u_r \times \overrightarrow{AP}} =\begin {bmatrix} \overrightarrow {i}& \overrightarrow{j} & \overrightarrow{k} \\ 3 & 1 & -2 \\ 1 & 4 & -3 \\ \end {bmatrix} = 5\overrightarrow {i} + 11 \overrightarrow {j} + 13 \overrightarrow {k}$

$|\overrightarrow{u_r \times \overrightarrow{AP}}| = \sqrt {5^2 + 11^2 + 13^2} = 3 \sqrt{35}$

$u_r = (3, 1, -2)$

$|u_r| = \sqrt{3^2 + 1^2 + )-2)^2} = \sqrt{14}$

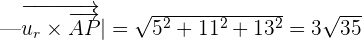
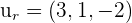
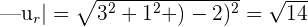
Put these values in the following formula to get the distance:

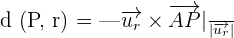
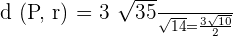
$d (P, r) = \frac {|\overrightarrow {u_r} \times \overrightarrow{AP}|} {|\overrightarrow{u_r}|}$

$d (P, r) = \frac {3 \sqrt{35}} {\sqrt{14}} = \frac {3 \sqrt{10}} {2}$

Example 2

Determine the distance from the point P = (2 , 1, −1) to the line 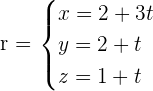$r = \begin{cases} x = 2 + 3t \\ y = 2 + t \\ z = 1 + t \end{cases}$ .

Solution

First, we have to calculate $\overrightarrow{u_r}$ .

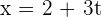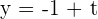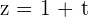We need to treat each of the $x = 2 + 3t$ , $y = -1 + t$ , and $z = 1 + t$ coefficients on the vector i, j, and k.

$= (2 + 3t) i, (2 + t)j, ( 1 + t)k$

= $2i + 3t i + 2j + tj + 1k, + tk$

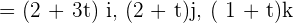
Now, we will make 2 groups. One group will have all the values that contain t and the other group will have all the values that do not contain t like this:

= (2i + 2j + k) + (3ti + tj + tk)

Now, we will factor out t from the second group like this:

= $2i + 2j + k + t (3i + j + k)$

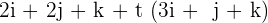
The coefficients in the first group tell us the point from which the line passes and the coefficients in the second group tell us about the direction vectors.

Hence, the direction numbers for the line are $\overrightarrow{u_r} = (3, 1, 1)$ and the coordinates of the point through which the lines passes are $\overrightarrow{A} = (2, 2, 1)$ .

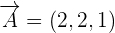We have to calculate the distance between the point P (2 , 1, −1) and point on the line A (2, 2, 1).

Since have both A and P, hence we can easily calculate $\overrightarrow{AP}$ like this:

$\overrightarrow{AP} = (2 - 2, 1 - 2, -1 - 1) = (0, -1, -2)$

Now, we will find the cross product of 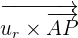$\overrightarrow{u_r \times \overrightarrow{AP}}$ using determinant:

$\overrightarrow{u_r \times \overrightarrow{AP}} =\begin {bmatrix} \overrightarrow {i}& \overrightarrow{j} & \overrightarrow{k} \\ 3 & 1 & 1 \\ 0 & -1 & -2 \\ \end {bmatrix} = -\overrightarrow {i} + 6 \overrightarrow {j} - 3 \overrightarrow {k}$

$|\overrightarrow{u_r \times \overrightarrow{AP}}| = \sqrt {(-1)^2 + (6)^2 + (-3)^2} = \sqrt{46}$

$u_r = (3, 1, 1)$

$|u_r| = \sqrt{3^2 + 1^2 + 1^2} = \sqrt{11}$

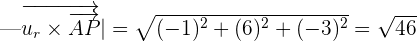
Put these values in the following formula to get the distance:

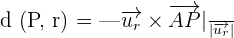
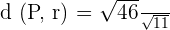
$d (P, r) = \frac {|\overrightarrow {u_r} \times \overrightarrow{AP}|} {|\overrightarrow{u_r}|}$

$d (P, r) = \frac {\sqrt{46}} {\sqrt{11}}$

Example 3

Determine the distance from the point P = (3 , 1, 2) to the line $r = \begin{cases} x = 1 + 3t \\ y = 4 + t \\ z = 1 + 4t \end{cases}$

Solution

First, we have to calculate $\overrightarrow{u_r}$ .

We need to treat each of the 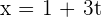$x = 1 + 3t$ , $y = 4 + t$ , and $z = 1 + 4t$ coefficients on the vector i, j, and k.

$= (1 + 3t) i, (4 + t)j, ( 1 + 4t)k$

= $i + 3t i + 4j + tj + 1k, + 4tk$

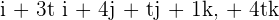
Now, we will make 2 groups. One group will have all the values that contain t and the other group will have all the values that do not contain t like this:

= (i + 4j + k) + (3ti + tj + 4tk)

Now, we will factor out t from the second group like this:

= $(i + 4j + k) + t (3i + j + 4k)$

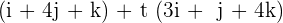
The coefficients in the first group tell us the point from which the line passes and the coefficients in the second group tell us about the direction vectors.

Hence, the direction numbers for the line are 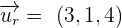$\overrightarrow{u_r} = (3, 1, 4)$ and the coordinates of the point through which the lines passes are $\overrightarrow{A} = (1, 4, 1)$ .

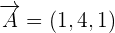We have to calculate the distance between the point P (3 , 1, 2) and point on the line A (1, 4, 1).

Since have both A and P, hence we can easily calculate $\overrightarrow{AP}$ like this:

$\overrightarrow{AP} = (1 - 3, 4 - 1, 1- 2) = (-2, 3, -1)$

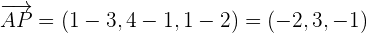
Now, we will find the cross product of $\overrightarrow{u_r} \times \overrightarrow{AP}$ using determinant:

$\overrightarrow{u_r} \times \overrightarrow{AP} =\begin {bmatrix} \overrightarrow {i}& \overrightarrow{j} & \overrightarrow{k} \\ 3 & 1 & 4 \\ -2 & 3 & -1 \\ \end {bmatrix} = 13\overrightarrow {i} + 5\overrightarrow {j} - 11 \overrightarrow {k}$

$|\overrightarrow{u_r} \times \overrightarrow{AP}| = \sqrt {(13)^2 + (5)^2 + (-11)^2} = \sqrt{315}$

$u_r = (3, 1, 4)$

$|u_r| = \sqrt{3^2 + 1^2 + 4^2} = \sqrt{26}$

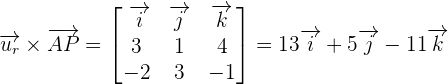
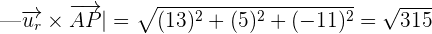
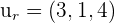
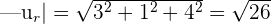
Put these values in the following formula to get the distance:

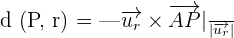
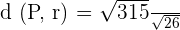
$d (P, r) = \frac {|\overrightarrow {u_r} \times \overrightarrow{AP}|} {|\overrightarrow{u_r}|}$

$d (P, r) = \frac {\sqrt{315}} {\sqrt{26}}$

Example 4

Determine the distance from the point P = (1, 2, 3) to the line 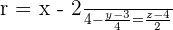$r = \frac {x - 2}{4} - \frac {y - 3}{4} = \frac {z - 4}{2}$

Solution

Here, A = (2, 3, 4) and $\overrightarrow{u_r}$ = (4, 4, 2)

$\overrightarrow {AP} = (1- 2, 3 - 2, 3 - 4) = (-1, -1, -1)$

$\overrightarrow{u_r} \times \overrightarrow{AP} =\begin {bmatrix} \overrightarrow {i}& \overrightarrow{j} & \overrightarrow{k} \\ -1 & -1 & -1 \\ 4 & 4 & 2 \\ \end {bmatrix} = -2\overrightarrow {i} + 2\overrightarrow {j}$

$|\overrightarrow{u_r} \times \overrightarrow{AP}| = \sqrt {(-2)^2 + (2)^2 + (0)^2} = \sqrt{8}$

$|u_r| = \sqrt {4^2 + 4^2 + 2^2} = \sqrt{6}$

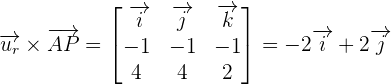
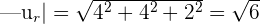
Put these values in the following formula to get the distance:

$d (P, r) = \frac {|\overrightarrow {u_r} \times \overrightarrow{AP}|} {|\overrightarrow{u_r}|}$

$d (P, r) = \frac {2 \sqrt{2}} {\sqrt{6}} = \frac {\sqrt{2}} {3}$

Example 5

Determine the distance from the point P = (2, 2, 4) to the line 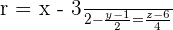$r = \frac {x - 3}{2} - \frac {y - 1}{2} = \frac {z - 6}{4}$

Solution

Here, A = (3, 1, 6) and $\overrightarrow{u_r}$ = (2, 2, 4)

$\overrightarrow {AP} = (2 - 3, 2 - 1, 4 - 6) = (-1, 1, -2)$

$\overrightarrow{u_r} \times \overrightarrow{AP} =\begin {bmatrix} \overrightarrow {i}& \overrightarrow{j} & \overrightarrow{k} \\ 2 & 2 & 4 \\ -1 & 1 & -2 \\ \end {bmatrix} = -8\overrightarrow {i} + 4\overrightarrow {j}$

$|\overrightarrow{u_r} \times \overrightarrow{AP}| = \sqrt {(-8)^2 + (4)^2 + (0)^2} = \sqrt{80}$

$|u_r| = \sqrt {2^2 + 2^2 + 4^2} = \sqrt{24}$

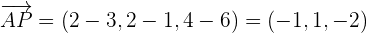
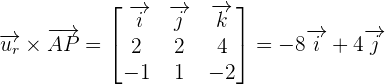
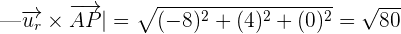
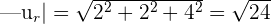
Put these values in the following formula to get the distance:

$d (P, r) = \frac {|\overrightarrow {u_r} \times \overrightarrow{AP}|} {|\overrightarrow{u_r}|}$

$d (P, r) = \frac {\sqrt{80}} {\sqrt{24}} \approx 1.825$

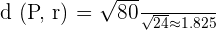
Find various Maths tuition on Superprof.

The platform that connects tutors and students

Did you like this article? Rate it!

4.00 (2 rating(s))

Emma

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.

Point-Line Distance

Distance Between Point and the Line

Example 1

Solution

Example 2

Solution

Example 3

Solution

Example 4

Solution

Example 5

Solution

Angle Between Two Planes

Distance Between a Point and a Plane

Angle Between Line and Plane

Line-Line Angle

Calculation of Areas and Volumes

Distance Between Two Lines

Distance Formulas

Problems of Distances, Areas and Volumes

Cancel reply

Point-Line Distance

Distance Between Point and the Line

Example 1

Solution

Example 2

Solution

Example 3

Solution

Example 4

Solution

Example 5

Solution

Theory

Angle Between Two Planes

Distance Between a Point and a Plane

Angle Between Line and Plane

Line-Line Angle

Calculation of Areas and Volumes

Distance Between Two Lines

Formulas

Distance Formulas

Exercises

Problems of Distances, Areas and Volumes

Cancel reply