Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10

Exercise 1
Find the area of the triangle whose vertices are the points A = (1, 1, 1), B = (3, 2, 1) and C = (−1, 3, 2).
Exercise 2
Find the volume of the tetrahedron whose vertices are the points A = (0,0,0), B = (2, 1, 3), C = (−1, 3, 1) and D = (4, 2, 1).
Exercise 3
Given the line 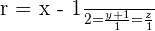 and the plane
and the plane 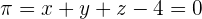 , find the equation of the line, s, which is the orthogonal projection of r on π.
, find the equation of the line, s, which is the orthogonal projection of r on π.
Exercise 4
Calculate the distance between the following lines:

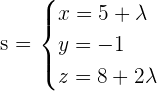
Exercise 5
Find the symmetric point of Point A = (3, 2, 1) to the plane 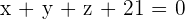 .
.
Exercise 6
Calculate the area of the triangle whose vertices are the points of intersection of the plane 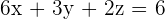 with the coordinate axes.
with the coordinate axes.
Exercise 7
Given the plane 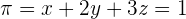 and the point A = (1, 1, 1), calculate the coordinates of the base (endpoint) of the perpendicular from A to the plane.
and the point A = (1, 1, 1), calculate the coordinates of the base (endpoint) of the perpendicular from A to the plane.
Exercise 8
Determine the equation of the plane π that is 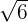 distant from the origin and is parallel to the plane
distant from the origin and is parallel to the plane 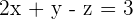 .
.
Exercise 9
Find the distance between the point A = (3, 2, 7) and the line of the first octant (+,+,+).
Exercise 10
Calculate the area of the square whose sides are on the lines:
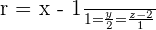
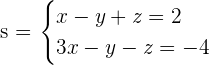
Solution of exercise 1
Find the area of the triangle whose vertices are the points A = (1, 1, 1), B = (3, 2, 1) and C = (−1, 3, 2).
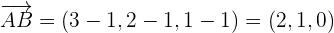
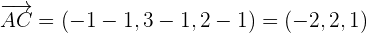
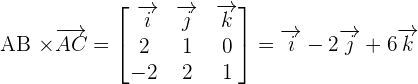
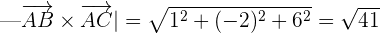
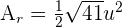
Solution of exercise 2
Find the volume of the tetrahedron whose vertices are the points A = (0,0,0), B = (2, 1, 3), C = (−1, 3, 1) and D = (4, 2, 1).
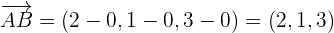
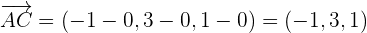

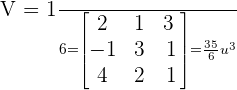
Solution of exercise 3
Given the line 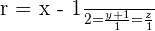 and the plane
and the plane 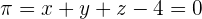 , find the equation of the line, s, which is the orthogonal projection of r on π.
, find the equation of the line, s, which is the orthogonal projection of r on π.
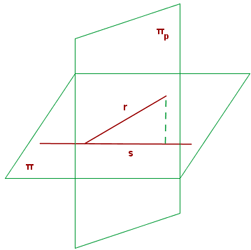
The line, s, is the intersection of the plane, π, with the plane, πp, that contains the line, r, and it is perpendicular to π.
The plane, πp, is determined by the point A = (2, −1, 0), the vector (2, 1, 1) and the normal vector, (1, 1, 1), of the perpendicular plane π.
Find various Maths tuition on Superprof.


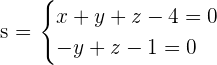
Solution of exercise 4
Calculate the distance between the following lines:
Calculate the distance between the following lines:


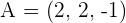
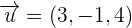
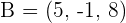
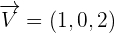
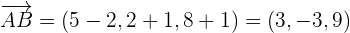
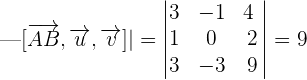

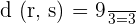
Solution of exercise 5
Find the symmetric point of Point A = (3, 2, 1) to the plane 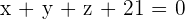 .
.
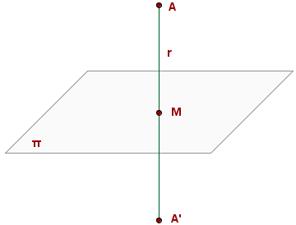
First, compute r, which is the line that passes through Point A and is perpendicular to π.
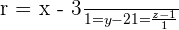
Then, find the point of intersection of the line r and the plane π.


Given the coordinates of the midpoint of the line segment, the endpoint A' can be found.
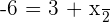
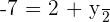

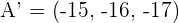
Solution of exercise 6
Calculate the area of the triangle whose vertices are the points of intersection of the plane 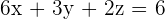 with the coordinate axes.
with the coordinate axes.
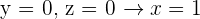



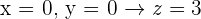
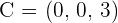
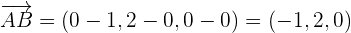

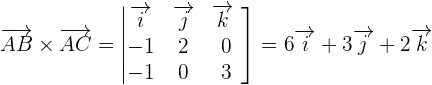
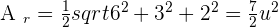
Solution of exercise 7
Given the plane 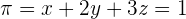 and the point A = (1, 1, 1), calculate the coordinates of the base (endpoint) of the perpendicular from A to the plane.
and the point A = (1, 1, 1), calculate the coordinates of the base (endpoint) of the perpendicular from A to the plane.
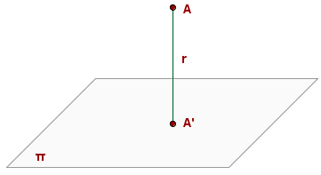

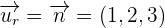

The foot of the perpendicular is the point of intersection between the plane and the line.
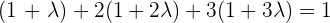
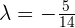
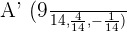
Solution of exercise 8
Determine the equation of the plane π that is 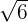 distant from the origin and is parallel to the plane
distant from the origin and is parallel to the plane 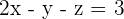 .
.
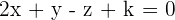

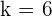
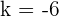
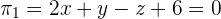
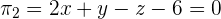
Solution of exercise 9
Find the distance between the point A = (3, 2, 7) and the line of the first octant (+,+,+).

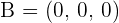




Solution of exercise 10
Calculate the area of the square whose sides are on the lines:
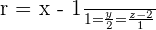
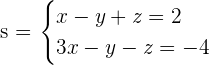
Line r.
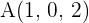
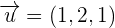
Line s.
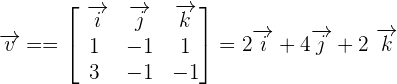
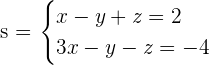
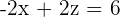
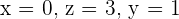
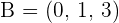
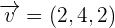
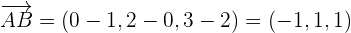
The distance of r to s is equal to the distance of the point B to the line r.

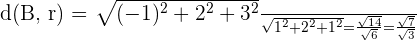
The side of the square is equal to the distance between the lines r and s.














I WANT TO CONTINUE WITH SOLVED PROBLEMS OF APPLICATION OF CROSS PRODUCTS OF VECTORS