Chapters
In this article, we will discuss how to find the angle between two lines.

Angle Between Two Lines
When two lines intersect each other, then two pairs of angles are formed that are opposite to each other. These angles are known as vertical angles.
If a line bisects another line, then we say that the lines are perpendicular to each other. In this case, the angles formed by intersection of lines are equal to  .
.
Formula to Calculate Angle Between Two Lines
Now, let us see what is the formula to calculate the angle between two lines when the lines are not perpendicular to each other.

Here, 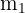 refers to the slope of the line 1 and
refers to the slope of the line 1 and  refers to the slope of the line 2.
refers to the slope of the line 2.
While finding the angle between two lines using the above formula keep the following things in mind:
- The angle between the two intersecting lines PQ and RS is either acute or obtuse depending on the positive or negative value of
 .
. - When two straight lines intersect each other, then the angle between these lines is acute.
- The formula
 is not applicable to the two intersecting lines that are parallel to the y-axis. This is because of the fact that we cannot determine the slope of the lines parallel to y-axis.
is not applicable to the two intersecting lines that are parallel to the y-axis. This is because of the fact that we cannot determine the slope of the lines parallel to y-axis.
The angle 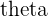 between two intersecting lines is shown in the diagram below:
between two intersecting lines is shown in the diagram below:

In the next section, we will solve couple of examples in which we will find angle between two lines using the formula discussed above.
Example 1
If P (3, 4), Q (2, 5) and R (-6, 8) are three points, then find the angle between the straight lines PQ and QR.
Solution
We will use the following formula to compute the angles between the lines PQ and QR.

You can see that in the above formula, we require 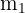 and
and  . Let suppose line PQ is line 1, having a slope of
. Let suppose line PQ is line 1, having a slope of 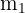 and QR is line 2 which has a slope of
and QR is line 2 which has a slope of  .
.
The coordinates of points P and Q are (3,4) and (2, 5) respectively. First, we will calculate 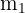 using the following formula:
using the following formula:
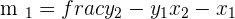

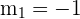
The coordinates of points Q and R are (2, 5) and (-6, 8) respectively. Now, we will compute the value of  using the same formula.
using the same formula.
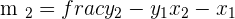
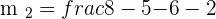

Now, we will put the value of 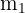 and
and  in the formula to get the required angle.
in the formula to get the required angle.

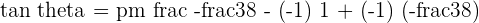
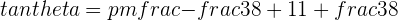



Hence, the angle between the lines PQ and QR is of the measure 24.44 degrees.
Example 2
If A (2, 5), B (7, 6) and C (-3, 1) are three points, then find the angle between the straight lines AB and BC.
Solution
We will use the following formula to compute the angles between the lines AB and BC.

You can see that in the above formula, we require 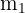 and
and  . Let suppose line AB is line 1, having a slope of
. Let suppose line AB is line 1, having a slope of 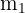 and BC is line 2 which has a slope of
and BC is line 2 which has a slope of  .
.
The coordinates of points A and B are (2, 5) and (7, 6) respectively. First, we will calculate 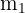 using the following formula:
using the following formula:
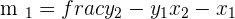
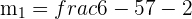

The coordinates of points B and C are (7, 6) and (-3, 1) respectively. Now, we will compute the value of  using the same formula.
using the same formula.
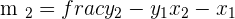
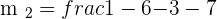
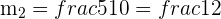
Now, we will put the value of 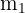 and
and  in the formula to get the required angle.
in the formula to get the required angle.


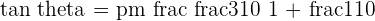



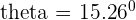
Hence, the angle between the lines AB and BC is of the measure 15.26 degrees.
Example 3
Find the angle between the lines of the following equations:
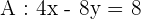
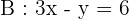
Solution
The equations of the lines A and B are given in the standard form. We have to convert these equations in slope intercept form to determine the slope.
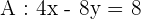
Divide both sides by 4 to get the following equation:
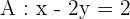
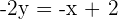
Divide both sides by -2:

Hence, the slope of this equation is 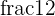
Now, we will convert the second equation in slope intercept form:
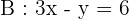
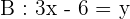
The slope of equation B is 3.
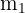 is equal to
is equal to 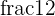 and
and  is equal to 3.
is equal to 3.

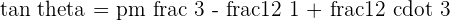


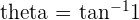
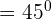
Hence, the angle between two lines A and B is 45 degrees.
Example 4
Find the angle between the lines of the following equations:
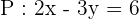

Solution
The equations of the lines P and Q are given in the standard form. We have to convert these equations in slope intercept form to determine the slope.
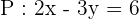
P : 
Divide both sides by -3:
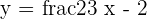
Hence, the slope of this equation is 
Now, we will convert the second equation in slope intercept form:

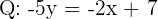
Divide both sides by -5:
Q: y = 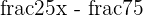
The slope of equation Q is 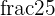 .
.
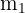 is equal to
is equal to  and
and  is equal to
is equal to 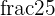 .
.

Substitute the values of slopes in the above equation:
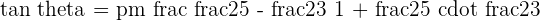
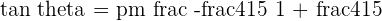
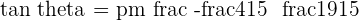


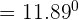
Hence, the angle between two lines P and Q is 11.89 degrees.
Example 5
Find the angle between the lines of the following equations:
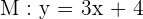
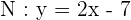
Solution
The equations of the lines M and N are already in the slope intercept form, i.e.  . Hence, we can easily find the slopes of the lines like this:
. Hence, we can easily find the slopes of the lines like this:
Slope of the line M = 
Slope of the line N = 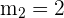
Use the following formula to calculate the angle between the lines M and N.

Substitute the values of slopes in the above equation:

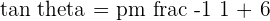
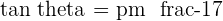
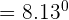
Hence, the angle between two lines M and N is 8.13 degrees.
Find various Maths tutors on Superprof.













I WANT TO CONTINUE WITH SOLVED PROBLEMS OF APPLICATION OF CROSS PRODUCTS OF VECTORS