Chapters

Distance Between a Point and a Plane
In this lesson, we will see how to compute the distance between a point and a plane. We will also see how to compute the distance between two parallel lines and planes.
"The shortest distance from a point to a plane is equal to the length of the perpendicular which originates from the point and joins the plane"
In other words, we can say that the shortest distance between a point and a plane is the length of the perpendicular line from the point to a plane.
Formula to Calculate the Distance Between a Point and a Plane
Let suppose there is a plane,  , and point P as shown below:
, and point P as shown below:


The distance between  and P will be a perpendicular line drawn from point P to the plane
and P will be a perpendicular line drawn from point P to the plane  . This distance can be calculate by using the following formula:
. This distance can be calculate by using the following formula:
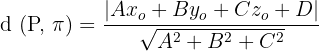
The distance from a point, P, to a plane, π, is the smallest distance from the point to one of the infinite points on the plane. Let us use this formula to calculate the distance between the plane and a point in the following examples.
Example
Calculate the distance from the point P = (3, 1, 2) and the planes 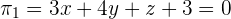 and
and 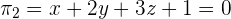
Solution
Part a
Use the following formula to compute the distance between the point and the plane. First, we will compute the distance between  and P.
and P.
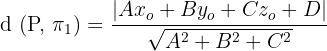
Substitute A = 3, b = 4, C = 1, and D = 3 in the above formula:
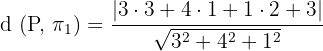
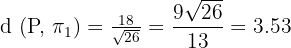
Part b
Now, we will compute the distance between 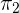 and point P. Use the following formula to compute the distance between the point and the plane.
and point P. Use the following formula to compute the distance between the point and the plane.
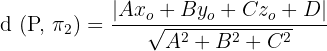
Substitute A = 1, B = 2, C = 3, and D = 1 in the above formula:
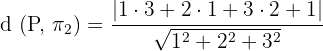
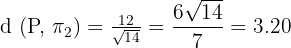
Distance Between Parallel Lines
One of the important elements in three-dimensional geometry is a straight line. In a Cartesian plane, the relationship between two straight lines varies because they can merely intersect each other, be perpendicular to each other, or can be the parallel lines. When two lines intersect each other, the distance between them is zero. The distance between two parallel lines is always the same. The slopes of parallel lines are always equal.
You may be wondering how to compute the distance between two parallel lines? Well, in this section, we will discuss how to compute the distance between two parallel lines.
The shortest distance between two parallel lines is equal to the length of the perpendicular between them. The location of the points does not matter. The only thing that matters is that the two points should be on the lines. Suppose there are two parallel lines  and
and 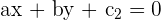 . The distance between these two lines can be calculated by the following formula:
. The distance between these two lines can be calculated by the following formula:
Find various Maths tutor near me on Superprof.
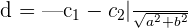
Example
Compute the distance between the following two parallel lines.
a) 2x + 2y + 3 = 0 and 2x + 2y + 5 = 0
b) x + 3y = - 6 and 3x + 9 y = -3
Solution
Part a
Here,  and
and 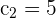 . Substitute these values in the formula below to get the distance:
. Substitute these values in the formula below to get the distance:
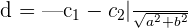
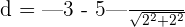
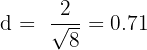
Part b
First, we will convert the above two lines into the form 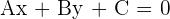 .
.
Line 1 = 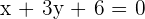
Line 2 = 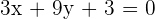
To make the coefficients equal we will divide the equation of the line 2 by the constant 3. The resulting equation will be:

Substitute 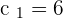 and
and  in the formula below:
in the formula below:
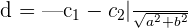
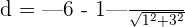
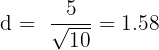
Distance Between Two Parallel Planes
The distance between two planes that are parallel to each other can be comprehended by considering the shortest distance between the surfaces of the two planes. If the planes are not parallel, then they will intersect each other. If two planes intersect each other, then the distance between them is zero. Before finding the distance, first, you have to determine if the two planes are parallel or not.
"The distance between two parallel planes is the distance from any point from a plane to another point on the other plane"
Let suppose the two planes have the following equations:
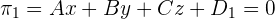
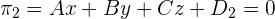
The formula for computing the distance between these two planes is given below:
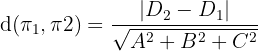
The following five steps should be followed while computing the distance between two parallel planes.
Steps to Compute the Distance Between Two Parallel Planes
Step 1
Ensure that the equations of the planes are written in the standard form. The equation of the plane in its standard form is given below:
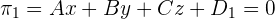
Step 2
In this step, you determine whether the two planes are parallel or not. This is because if the planes are not parallel, then they would definitely intersect each other at some point. The distance between perpendicular planes is zero.
To determine whether the planes are parallel or not, consider the following ratios:
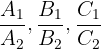
If the lines are parallel, then these ratios are equal. Mathematically, we write it as:
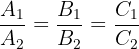
Step 3
Identify the values of the coefficients A, B, and C. If the two lines do not have the same coefficients, then you can make them equal by multiplying or dividing either equation by a constant.
Step 4
In this step, you will derive the values of  and
and 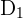 from the two equations.
from the two equations.
Step 5
Substitute these values in the formula for computing the distance between two parallel planes. This formula is given above in this article.
Example
Compute the distance between the following two parallel planes:
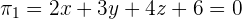
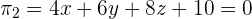
Solution
Follow these steps to compute the distance between the above two planes.
Step 1
First, we need to convert the equations into the standard form. In this example, the equations of the planes are already given in the standard form, therefore we will do nothing in this step and proceed to the second step.
Step 2
In this step, we will see whether the two planes are parallel or not. To determine this, we need to look at the certain ratios.
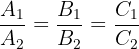
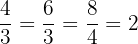
The ratios are equal which depicts that the planes are parallel.
Step 3
Now, we will find the values of coefficients A, B and C. The two equations are:
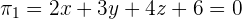
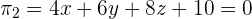
We will divide the equation of the plane 2 by a constant 2 to get the same coefficients in both the equations:
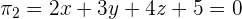
Step 4
In this step, we will derive the values of 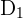 and
and  from the two equations.
from the two equations.
In this example, 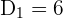 and
and 
Step 5
Substitute all the values in the below formula to compute the distance between two parallel planes:
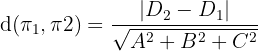
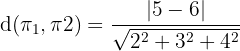
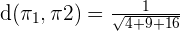
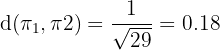













I WANT TO CONTINUE WITH SOLVED PROBLEMS OF APPLICATION OF CROSS PRODUCTS OF VECTORS