Chapters
In this article, we will discuss how to find the distance between two parallel and skew lines.
The shortest distance between two lines refer to how far away two lines are located from each other. In other words, we can say that the shortest distance between two lines in a plane is the minimum distance between any two points that are present on both the lines. The shortest distance is the measure of the length of a perpendicular line between two lines.
In geometry, we come across different lines such as parallel lines and skew lines. We have formulas to calculate the distance between two parallel and skew lines. In this article, we will focus on using formulas to find the minimum distance between these types of lines.

Distance Between Parallel Lines
What are parallel lines?
Two lines that are parallel never meet each other and they have the same slopes.
How to find the distance between two parallel lines?
Before proceeding to discuss the method to find the distance between two parallel lines, let us first see what is meant by the distance.
- See whether the equations are given in slope intercept form or not
- Slope value should be common for both the lines if they are given in the slope intercept form. Determine the values of
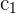 and
and 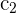
- After finding the values, substitute them in the slope-intercept equation to calculate y.
- In the last step, substitute all the values in the distance formula discussed below to find the distance between two parallel lines
The formula for distance between two parallel lines is given below if the lines are in the slope intercept form. Remember that the slope intercept form of the line is  .
.

Here, 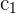 is the constant of line 1 and
is the constant of line 1 and 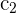 is the constant of line 2.
is the constant of line 2.  represents the slope of
represents the slope of
If the equations of the parallel lines are given in the 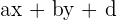 , then the formula is slightly different than the first one:
, then the formula is slightly different than the first one:
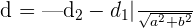
Example 1
Find the distance between the parallel lines having the following equations:
Line 1 :
Line 2 : 
Solution
These lines have the same slopes, so we will use the following formula to compute the distance between them:

Here, 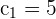 ,
, 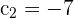 , and
, and  . Substitute these values in the above formula:
. Substitute these values in the above formula:
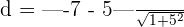
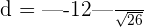
 units
units
Hence, the distance between two lines is 2.35 units.
Example 2
Find the distance between the parallel lines having the following equations:
Line 1 : 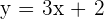
Line 2 : 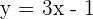
Solution
These lines have the same slopes, so we will use the following formula to compute the distance between them:

Here,  ,
, 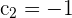 , and
, and 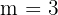 . Substitute these values in the above formula:
. Substitute these values in the above formula:
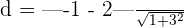
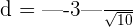
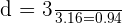 units
units
Hence, the distance between two lines is 0.94 units.
Example 3
Find the distance between the following two parallel lines:
Line 1 : 
Line 2 : 
Solution
Since the equations are given in the form 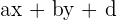 , hence we will use the following formula to compute the distance:
, hence we will use the following formula to compute the distance:
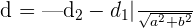
Here,  ,
, 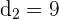 ,
, 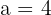 and
and  . Substitute these values in the above formula to get the distance:
. Substitute these values in the above formula to get the distance:
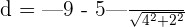
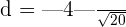

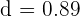 units
units
Hence, the distance between these lines is 0.89 units.
Example 4
Find the distance between the following two parallel lines:
Line 1 : 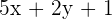
Line 2 : 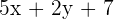
Solution
Since the equations are given in the form 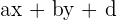 , hence we will use the following formula to compute the distance:
, hence we will use the following formula to compute the distance:
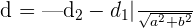
Here,  ,
,  ,
,  and
and  . Substitute these values in the above formula to get the distance:
. Substitute these values in the above formula to get the distance:

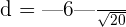
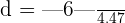
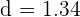 units
units
Hence, the distance between these lines is 1.34 units.
Example 5
Find the distance between the following two parallel lines:
Line 1 : 
Line 2 : 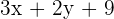
Solution
Since the equations are given in the form 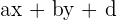 , hence we will use the following formula to compute the distance:
, hence we will use the following formula to compute the distance:
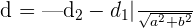
Here, 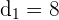 ,
, 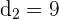 ,
,  and
and  . Substitute these values in the above formula to get the distance:
. Substitute these values in the above formula to get the distance:
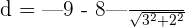
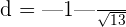
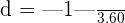
 units
units
Hence, the distance between these lines is 0.27 units.
Example 6
Find the distance between the following two parallel lines:
Line 1 : 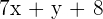
Line 2 : 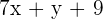
Solution
Since the equations are given in the form 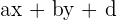 , hence we will use the following formula to compute the distance:
, hence we will use the following formula to compute the distance:
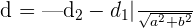
Here, 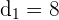 ,
, 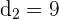 ,
, 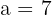 and
and  . Substitute these values in the above formula to get the distance:
. Substitute these values in the above formula to get the distance:



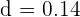 units
units
Hence, the distance between these lines is 0.14 units.
Distance Between Skew Lines
These lines do not intersect each other at any point, but they are also not parallel to each other. These lines are also called agonic lines and most of the time these lines exist in three or more dimensions. In the figure below, the lines r and s are skew lines.
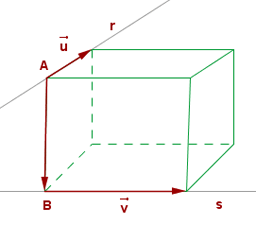
The general formula to calculate the distance between two skew lines of the form 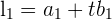 and
and  is given below:
is given below:
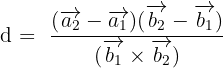
Example
Find the distance between the following lines:
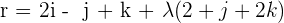 and
and 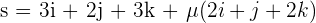
Solution
Here, 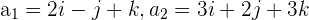 and values of
and values of 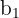 and
and 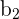 are same, i.e.,
are same, i.e.,  . We will use the following formula to compute the distance:
. We will use the following formula to compute the distance:
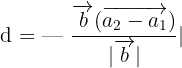



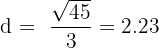
Hence, the distance between the lines is 2.23 units.
Find various Maths tuition on Superprof.













I WANT TO CONTINUE WITH SOLVED PROBLEMS OF APPLICATION OF CROSS PRODUCTS OF VECTORS