Chapters

Definition of Rational Numbers
Rational numbers are numbers that can be reduced to a ratio of two integers  and
and  , where
, where  cannot be
cannot be 
{ with
with 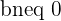 }
}
They are called Rational because of the fact that they are a ratio or quotient of two integers. 'Ratio' is the root of rational and that's what it means in this sense, the ability to be represented as a ratio.
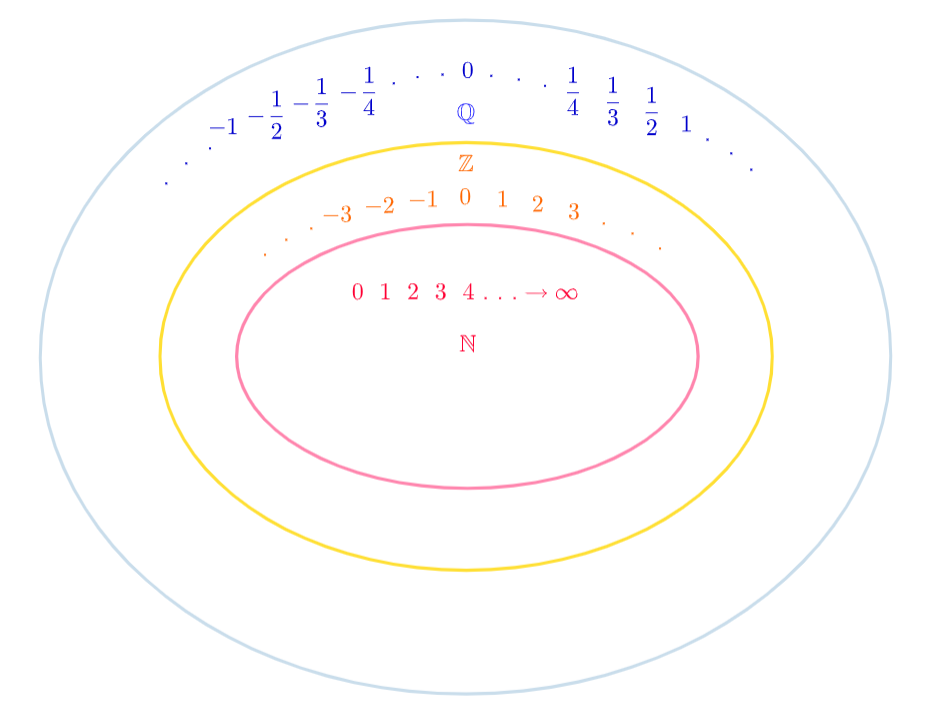
The total group of all Rational Numbers is denoted by 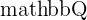 . The Natural Numbers
. The Natural Numbers 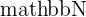 and Integers
and Integers 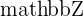 are both subsets of the Rational Numbers. This means that every Natural number and every Integer is also a Rational number
are both subsets of the Rational Numbers. This means that every Natural number and every Integer is also a Rational number
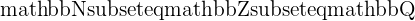
where  means 'is a subset of'.
means 'is a subset of'.
Every Rational number can be represented as a ratio of two integers. Rational numbers have the property of having a finite or infinitely repeating equivalent decimal value.
Examples of Rational Numbers and their Equivalent Decimal Values
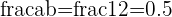
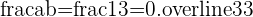
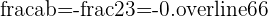

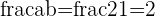
Notice that the integer  is also the fraction
is also the fraction  or
or 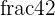 or
or 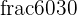 . All of these are just alternate forms of the number
. All of these are just alternate forms of the number  .
.
Rational Number Diagram
More about Rational Numbers
Any Natural number or Integer  is the ratio of that number
is the ratio of that number  to
to 
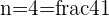
The Rational Numbers are not just the numbers known as fractions, although that is ultimately a property that each one shares.
We can imagine a fraction that includes an irrational number, which would not be a Rational number because it includes a number that is non-repeating and non-ending.
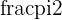 is an example of a fraction that is not Rational
is an example of a fraction that is not Rational
Rational numbers can come in many forms: Natural numbers, integers, decimals, ratios, fractions or quotients; any form of number that can be reduced to a ratio of integers.
Number Line Representation of Rational Numbers
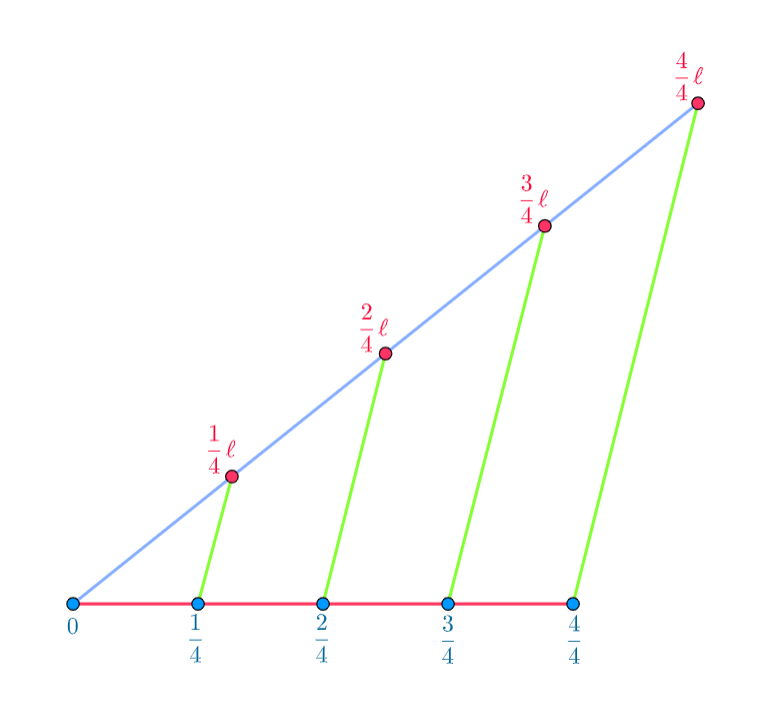
The Rational Numbers 'fill-up' some of the space between the Integers on the Number Line. We can divide any region from one integer to another integer into any amount of subdivisions we want.
We can subdivide the region between  and
and  into fifth's by marking off 4 points
into fifth's by marking off 4 points 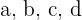 that will make 5 equal spaces in between
that will make 5 equal spaces in between
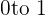

the 4 points 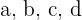 in between will be at
in between will be at
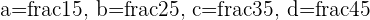
making 5 equally spaced segments between  and
and  of
of
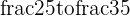
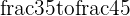
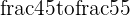
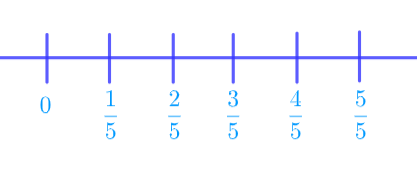
How to Divide a Line into Equal Segments
Summarise with AI:













