Importance of Sequences and Series in Real Life
Series and sequence have become a part of our lives. With the help of series and sequences, we can do many predictions. Let's create an example of a process industry. A reactor of a process industry has a fault. An engineer noted the fault and saw that after every five hours, the temperature of the reactor is decreasing by
. This will have an impact on the final product. Since it is a process industry, you can't shut it down until the critical situation. The engineer gives an alarm about it but the question is how much time do they have? Let's say the reactor was operating at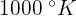
and the critical situation comes at
. This can be easily calculated by series and sequence. With the help of this concept, the engineer can estimate the total time they have to fix this reactor before shut down. This can save a lot of money for that process industry.
What is a Geometric Sequence?
Sequence and series have different types. The example has a different type of series called arithmetic series, however, in this blog, we want to focus on the geometric sequence. The Geometric sequence is the multiplication of all terms with a constant. Here is a sequence that represents geometric sequence:
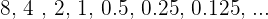
The relation of each term with the other is through a geometric sequence. The first term, which is
, becomes
in the second term. If we multiply
by
, we get the second term! Just to be on the safe side, let's multiply the second term by
again and then compare it to the third term.
Is this a coincidence? No! It is Maths! So, this geometric sequence has a common ratio of
. It is easy till here, right? Let's tackle some difficult ones! You are asked to find the
term of this sequence. Grab your calculators and start dividing the first term by
for about, 50 times! That is a lot of work right? Not to mention there is a high possibility that you forget the count while processing. You don't need to divide the first term by two for fifty times, you can use a simple formula that will calculate the value of the
term. Here is the formula:
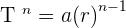
To understand this formula, let's try to understand the concept of a geometric sequence again. A geometric sequence or geometric progression is a sequence of numbers such that the ratios between successive terms is a constant r, called the common ratio. For better clarification, here is an example:
Find the common ratio of the following geometric series:
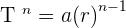
To find the common ratio, we will use the second term.
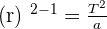
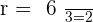
We did find the common ratio, however, let's be on safe side and check whether we found the right common ratio or not? First term =
Second term =
Third term =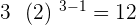
Fourth term =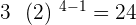
Fifth term =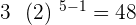
In conclusion, 
Nth Term of a Geometric Sequence
Let's discuss finding the
term again. There are two methods to find any of the
term, however, they have a condition.
1 If the 1st term is known.
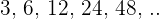
2 If the value that occupies any other term of the sequence is known.
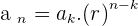
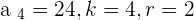
Geometric Series
Not only you can find terms, first term, common difference, and a few more, you can also find the sum of the series. A geometric series is the sum of a geometric sequence.
Compute the sum of the first 5 terms of the sequence:
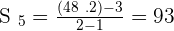
Infinite Geometric Series
One of the most important as well as most used concepts in the geometric sequence is the sum to infinity. If 
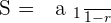
Calculate the sum of the terms of the sequence:
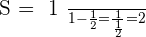
Product
Moreover, you can also find the product of n terms of a geometric progression.
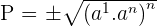
Calculate the product of the first 5 terms of the sequence:
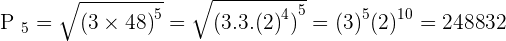
Summarise with AI:
Did you like this article? Rate it!
Loading...
I get it somehow, there are others who are unfamiliar and I have a hard time with it but it’s okay that I get it.
Thanks for sharing your thoughts! It’s completely normal to find some parts unfamiliar or more difficult than others. The important thing is that you’re making progress and understanding more as you practise. Keep going! 😊
At least I understood some of it, but there are others that I’m confused about and have a hard time understanding, but I get it.
Thanks for sharing! It’s great that you’ve understood some of it already. Don’t worry if a few parts are still confusing — keep practising and take your time with the trickier sections. You’ll get there! 😊
The lesson was a little difficult for me, especially the word problems, but the examples helped me understand it better.
Thanks for your feedback! Word problems can definitely be tricky, so we’re glad the examples helped make the lesson clearer. Keep practising — it gets easier with time! 😊
Thankyouuu po