Chapters
A Matrix is a set of numbers that are arranged in rows and columns. Basically, it is a rectangular array that is filled with numbers. The numbers that are filled inside a matrix are called elements of the matrix. Matrices are widely used in many applications such as engineering, statistics, web development, and a few more. Not to mention that matrices are mostly used in mathematics. In the past, matrices were mainly used for storing data or to calculate the determinants. Today, matrices are not just a method to store data but it has powered many applications such as computer graphics, solving equations that require a number of iterations and in many more.
A matrix is identified by its rows and columns. That is why matrices are written in the form of their rows and columns (like this 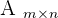 ). Take a look at the below matrix:
). Take a look at the below matrix:
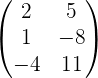
There are 3 rows and 2 columns in the above matrix hence this matrix will be called 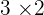 matrix. This is the standard way of writing a matrix. Here is the syntax of writing a matrix, "
matrix. This is the standard way of writing a matrix. Here is the syntax of writing a matrix, "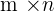 ". The "m" represents the number of rows while the "n" represents the number of columns. Below are some examples of matrices with their orders:
". The "m" represents the number of rows while the "n" represents the number of columns. Below are some examples of matrices with their orders:

Examples
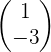
 matrix
matrix
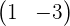
 matrix
matrix

 matrix
matrix
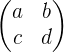
This type of matrix is called a square matrix. The condition of a square matrix is that the number of rows and columns should be equal. We always express the square matrix as the order of the matrix. Hence, the order of the above square matrix is " ".
".
In Nutshell
Each number in a matrix is an element. One element is distinguished from another by its position, that is to say, the row and column to which it belongs. The number of rows and columns of a matrix is called the dimension of a matrix. Thus, a matrix is of dimension: 2x4, 3x2, 2x5,... If the matrix has the same number of rows and columns, is said to be of order: 2, 3, ...
The set of matrices of m rows and n columns is denoted by Amxn or (aij), and any element within the matrix is in row i in column j, for aij.
Two matrices are equal when they have the same dimension and equal elements that occupy the same place in both.













I appreciate your work, thanks so much keep up the good work ✅
Hello Little P! Thanks very much for the positive feedback!
I didn’t get the same answer for the second question, ive also asked my friends and we all got the same answer it just didnt line up with yours. Apart from that, great website and thanks for the exercises.
Very nice and good explanation of matrix
Give some more examples of matrix
I want to more study about matrix that’s why I’m using Google