Finding the inverse of a matrix can be tricky but once understood properly, you can tackle any question. The multiplication of a matrix by its inverse is equal to the identity matrix. It means that when you multiply the original matrix with the inverse of that matrix, it will always result in the identity matrix.
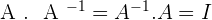
For example, you are asked to find the inverse of  . What you should do is reciprocate the number because inverse means negative exponent(
. What you should do is reciprocate the number because inverse means negative exponent(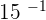 ), to make the exponent positive, you need to reciprocate the number(
), to make the exponent positive, you need to reciprocate the number(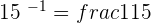 ). We do the same for matrix, let's say we have a matrix A, now the inverse of A will be
). We do the same for matrix, let's say we have a matrix A, now the inverse of A will be 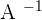 , however, how will you reciprocate the whole matrix? It isn't easy, that is why we have a method for finding the inverse of a matrix and it is called the Gaussian elimination method. Gaussian elimination method is not the only method to find the inverse of a matrix, there are a few more methods but this method is the easiest and that is why, in this lesson, we will cover how to use the Gaussian elimination method to find the inverse of a matrix.
, however, how will you reciprocate the whole matrix? It isn't easy, that is why we have a method for finding the inverse of a matrix and it is called the Gaussian elimination method. Gaussian elimination method is not the only method to find the inverse of a matrix, there are a few more methods but this method is the easiest and that is why, in this lesson, we will cover how to use the Gaussian elimination method to find the inverse of a matrix.

Properties of the Inverse Matrix
There are 4 properties of the inverse matrix which are listed below:
1. If a matrix is nonsingular then its inverse matrix will also be nonsingular
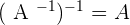
2. If two nonsingular matrices are multiplied with each other they will still produce a nonsingular matrix
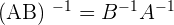
3. If a matrix is nonsingular then 
4. Suppose two matrics, A and B, with their product resulting in identity matrix,  , we can say that A and B matrices are inverses of each other.
, we can say that A and B matrices are inverses of each other.
Steps to Calculate the Inverse Matrix
Gaussian Elimination Method
A is a square matrix of order n. To calculate the inverse of A, denoted as 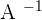 , follow these steps:
, follow these steps:
Step 1:
Construct a matrix of type 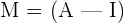 , that is to say, A is in the left half of M and the identity matrix I is on the right.
, that is to say, A is in the left half of M and the identity matrix I is on the right.
Consider an arbitrary 3x3 matrix:
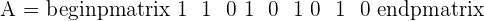
Place the identity matrix of order 3 to the right of Matrix M like below:
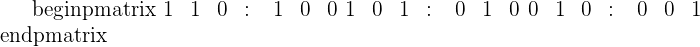
Step 2:
Using the Gaussian elimination method, transform the left half, A, to the identity matrix, located to the right, and the matrix that results in the right side will be the inverse of the matrix: 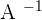 .
.

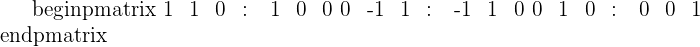


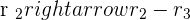
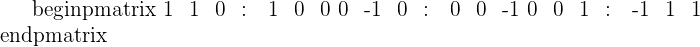

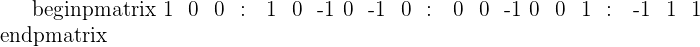


The inverse matrix is:
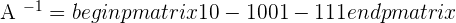
Example
Calculate the matrix inverse of:
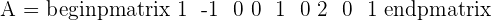
Construct a matrix of type M = (A | I).
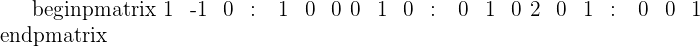
Using the Gaussian elimination method, transform the left half, A, in the identity matrix, located to the right, and the matrix that results in the right side will be the inverse of matrix : 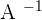 .
.
| r3 - 2r1 | r3 - 2r2 |
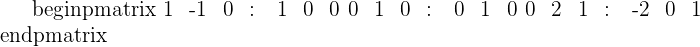 | 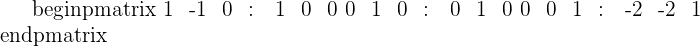 |
| r1 + r2 | Matrix Inverse |
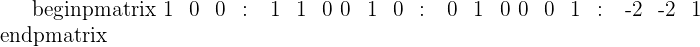 | 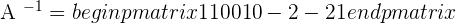 |
For what values of m in the matrix 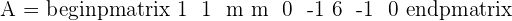 does not support an inverse?
does not support an inverse?
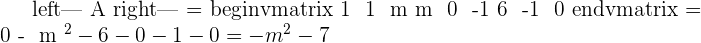

For any real value of m, there is the inverse  A-1.
A-1.
Calculating the matrix inverse for determinants
Summarise with AI:













I appreciate your work, thanks so much keep up the good work ✅
Hello Little P! Thanks very much for the positive feedback!
I didn’t get the same answer for the second question, ive also asked my friends and we all got the same answer it just didnt line up with yours. Apart from that, great website and thanks for the exercises.
Very nice and good explanation of matrix
Give some more examples of matrix
I want to more study about matrix that’s why I’m using Google