Chapters

Exercise 1
Calculate the rank of the matrix

Exercise 2
Calculate the rank of the matrix by the gaussian elimination method.

Exercise 3
Calculate the rank of the matrix by the gaussian elimination method.
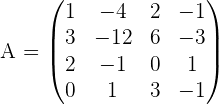
Exercise 4
Calculate the rank of the matrix by determinants.

Exercise 5
Calculate the rank of the matrix by determinants.
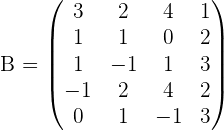
Exercise 6
Calculate the rank of the matrix by determinants.

Exercise 7
Calculate the rank of the matrix by determinants.

Solution of exercise 1
Calculate the rank of the matrix

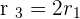
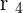 is null
is null
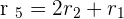
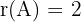
Solution of exercise 2
Calculate the rank of the matrix by the gaussian elimination method.



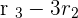
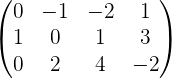
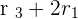

Therefore r(A) =2.
Solution of exercise 3
Calculate the rank of the matrix by the gaussian elimination method.
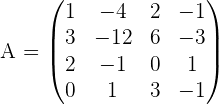
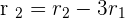
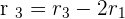

r(A) = 3.
Solution of exercise 4
Calculate the rank of the matrix by determinants.


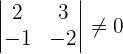

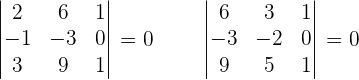
r(A) = 2
Solution of exercise 5
Calculate the rank of the matrix by determinants.



r(B) = 4
Solution of exercise 6
Calculate the rank of the matrix by determinants.

Remove the third column as it is zero, the fourth because it is proportional to the first and the fifth because it is the linear combination of the first and second: 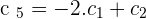
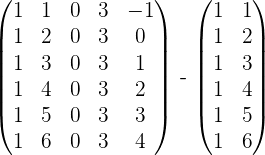

r(C) = 2
Solution of exercise 7
Calculate the rank of the matrix by determinants.

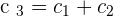


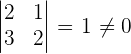
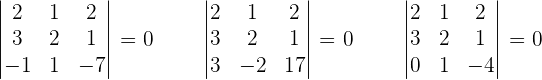
r(D) = 2













I appreciate your work, thanks so much keep up the good work ✅
Hello Little P! Thanks very much for the positive feedback!
I didn’t get the same answer for the second question, ive also asked my friends and we all got the same answer it just didnt line up with yours. Apart from that, great website and thanks for the exercises.
Very nice and good explanation of matrix
Give some more examples of matrix
I want to more study about matrix that’s why I’m using Google