Chapters
There are many things that you can do with a matrix such as addition of matrics, multiplication of matrices, etc., one of them is scalar matrix multiplication. To understand the scalar matrix multiplication, you need should know what is a matrix and different types of matrix. Scalar matrix multiplication isn't a complex operation, in fact, it is very easy to understand. Basically, it is an operation where a real number is multiplied by the elements of a matrix. In this lesson, you will learn about scalar matrix multiplication and its different properties.
Scalar matrix multiplication has a condition. The scalar number multiplied by the matrix should be a real number. Real number is a type of number which exists in real life, it contains many different numbers such as rational numbers, natural numbers, whole numbers, and a few more. The opposite of a real number is an imaginary number which clearly tells about a number that does not exist in real-life. Whenever a scalar number is multiplied to a vector or matrix, it "re-scales" the elements of the matrix or vector. In simple words, it changes the magnitude of the vector and matrix without changing its other characteristics such as dimension, and direction.
Suppose you are given a matrix,  and it is multiplied to a real number,
and it is multiplied to a real number,  . The product of the matrix and the real number will a new matrix but with the same dimension as
. The product of the matrix and the real number will a new matrix but with the same dimension as  (remember the "re-scaling" part). All the elements of the specific matrix will be multiplied by the real number and this will result in a new matrix.
(remember the "re-scaling" part). All the elements of the specific matrix will be multiplied by the real number and this will result in a new matrix.


Examples
1. 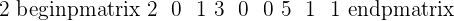

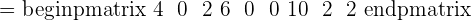
2. 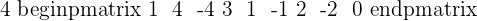


3. 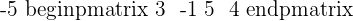
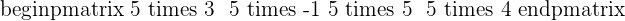

4. 

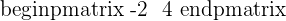
Properties
Property No.1: Associative
It doesn't matter what way you group, it will always result in the same. In simple words, the way in which the matrices are grouped does not change the result.

where 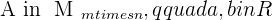
Property No.2: Distributive

where 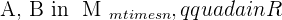
Property No.3: Multiplicative identity
This property states that if you multiply any matrix with an identity matrix, it will always result in the same matrix, the order of matrix doesn't matter.
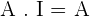
Where I is the identity matrix with the same order as matrix A and 
Property No.4: Multiplicative properties of zero
Any matrix that comes in contact with zero will always result in zero.
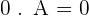
where 













I appreciate your work, thanks so much keep up the good work ✅
Hello Little P! Thanks very much for the positive feedback!
I didn’t get the same answer for the second question, ive also asked my friends and we all got the same answer it just didnt line up with yours. Apart from that, great website and thanks for the exercises.
Very nice and good explanation of matrix
Give some more examples of matrix
I want to more study about matrix that’s why I’m using Google