Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9

Exercise 1
Given the matrices:
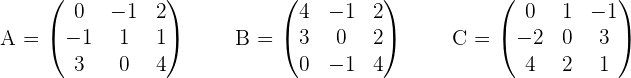
Calculate:
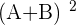 ;
;
 ;
;
 ;
;
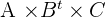 .
.
Exercise 2
Prove that: 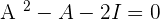 where:
where:
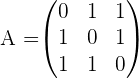
Exercise 3
Given the matrix 
Find:
1. 
2. 
3. 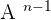
Exercise 4
Determine the matrix that is needed to premultiply by the matrix 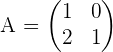 in order to obtain the matrix
in order to obtain the matrix 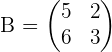 .
.
Exercise 5
Find all matrices that commute with the matrix:
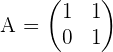
Exercise 6
Determine the matrices A and B that verify the system:
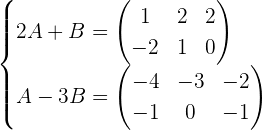
Exercise 7
A factory produces two models of washing machines, A and B, in three available finishes: N, L, and S. Model A is produced in 400 units in Finish N, 200 units in Finish L, and 50 units in Finish S. Model B is produced in 300 units in Finish N, 100 units in Finish L and 30 units in Finish S. Finish N takes 25 hours of workshop time to complete and 1 hour of administration. Finish L takes 30 hours of workshop time and 1.2 hours of administration. Finally, Finish S takes 33 hours of workshop time and 1.3 hours of administration.
1.Represent the information in two matrices.
2.Find a matrix that expresses the hours of workshop and administration time needed for each of the models.
Exercise 8
A furniture company manufactures three different models of shelves: A, B, and C. Each of these models is offered in both large and small sizes. Every day, the factory produces  large and
large and  small shelves in Type A,
small shelves in Type A,  large and
large and 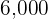 small shelves in Type B, and
small shelves in Type B, and 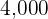 large and
large and 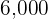 small shelves in Type C. Regardless of the type, each large shelf has
small shelves in Type C. Regardless of the type, each large shelf has  screws and
screws and  supporting brackets while each small shelf has
supporting brackets while each small shelf has  screws and
screws and  supporting brackets.
supporting brackets.
1. Represent this information in two matrices.
2. Find a matrix that represents the number of screws and supports brackets necessary for the daily production of each of the six model-sized shelves.
Exercise 9
Given the matrices:

Calculate the value of X in the following equations:
1. 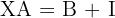
2. 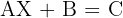
3. 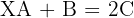
4. 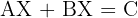
5. 
Solution of exercise 1
Given the matrices:
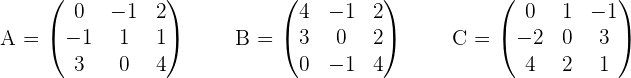
Calculate:
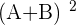 ;
;
 ;
;
 ;
;
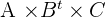 .
.
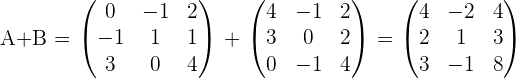
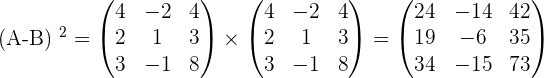
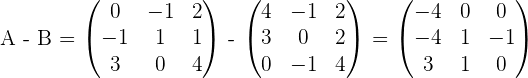
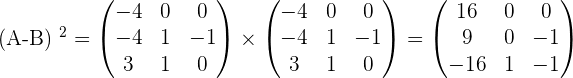
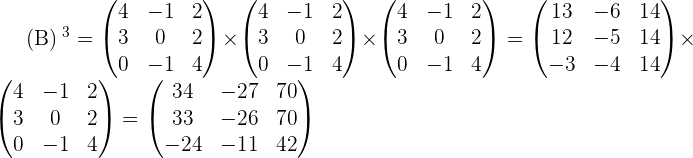
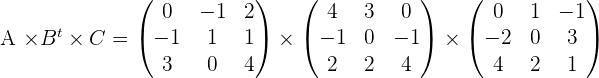

Solution of exercise 2
Prove that: 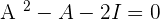 where:
where:
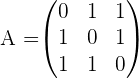
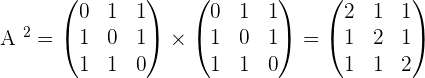
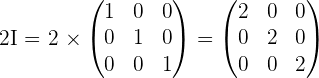

Solution of exercise 3
Given the matrix 
Find:
1. 
2. 
3. 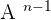
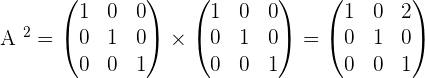
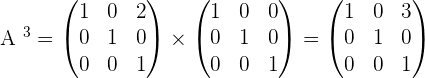

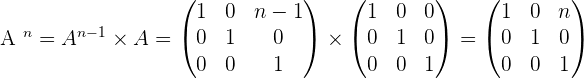
Solution of exercise 4
Determine the matrix that is needed to premultiply by the matrix 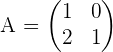 in order to obtain the matrix
in order to obtain the matrix 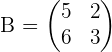 .
.

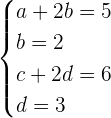
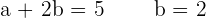
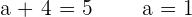
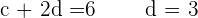


Solution of exercise 5
Find all matrices that commute with the matrix:
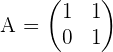
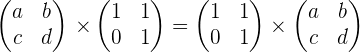

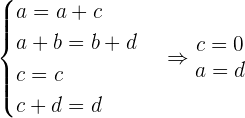
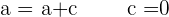

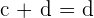
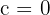
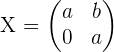
Solution of exercise 6
Determine the matrices A and B that verify the system:
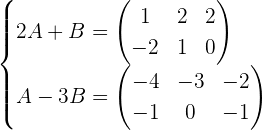
Multiply the second equation by −2

Add member to member

If the first equation is multiplied by 3 and the members are added, the result is:
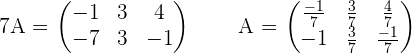
Solution of exercise 7
A factory produces two models of washing machines, A and B, in three available finishes: N, L, and S. Model A is produced in 400 units in Finish N, 200 units in Finish L, and 50 units in Finish S. Model B is produced in 300 units in Finish N, 100 units in Finish L and 30 units in Finish S. Finish N takes 25 hours of workshop time to complete and 1 hour of administration. Finish L takes 30 hours of workshop time and 1.2 hours of administration. Finally, Finish S takes 33 hours of workshop time and 1.3 hours of administration.
1.Represent the information in two matrices.
2.Find a matrix that expresses the hours of workshop and administration time needed for each of the models.
Matrix production:
Rows: Models A and B Columns: Completions N, L, S

Cost matrix in hours:
Rows: Finishes N, L, S Columns: Cost in hours: T, A
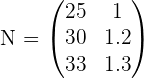
Matrix that expresses the hours of workshop and administration for each of the models:
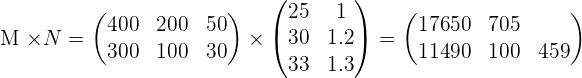
Solution of exercise 8
A furniture company manufactures three different models of shelves: A, B, and C. Each of these models is offered in both large and small sizes. Every day, the factory produces  large and
large and 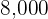 small shelves in Type A,
small shelves in Type A, 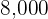 large and
large and 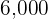 small shelves in Type B, and
small shelves in Type B, and 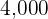 large and
large and 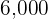 small shelves in Type C. Regardless of the type, each large shelf has
small shelves in Type C. Regardless of the type, each large shelf has  screws and
screws and  supporting brackets while each small shelf has
supporting brackets while each small shelf has  screws and
screws and  supporting brackets.
supporting brackets.
1. Represent this information in two matrices.
Rows: Models A, B, C Columns: Types L, S

Matrix elements of the shelves:
Rows: Types L, S Columns: T, S
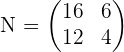
2. Find a matrix that represents the number of screws and supports brackets necessary for the daily production of each of the six model-sized shelves.
The matrix that expresses the number of screws and supporting brackets for each shelf model:

Solution of exercise 9
Given the matrices:

Calculate the value of X in the following equations:
1. 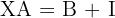
2. 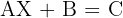
3. 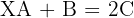
4. 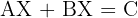
5. 
1. 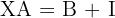
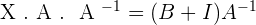
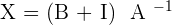
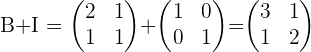
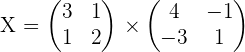

2. 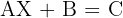
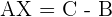
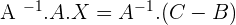

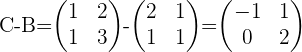
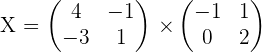

3. 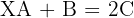
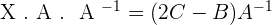
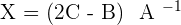


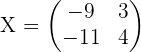
4. 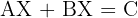


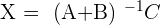
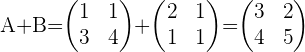
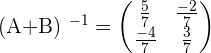
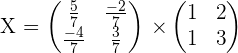

5. 



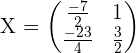













I appreciate your work, thanks so much keep up the good work ✅
Hello Little P! Thanks very much for the positive feedback!
I didn’t get the same answer for the second question, ive also asked my friends and we all got the same answer it just didnt line up with yours. Apart from that, great website and thanks for the exercises.
Very nice and good explanation of matrix
Give some more examples of matrix
I want to more study about matrix that’s why I’m using Google