Exercise 1
Calculate the matrix inverse by the gaussian elimination method.
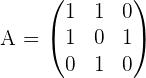
Exercise 2
Calculate the matrix inverse by the gaussian elimination method.
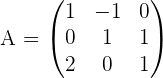
Exercise 3
Calculate the matrix inverse by determinants.
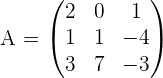
Exercise 4
For what values of m in the matrix
does not support an inverse?
Exercise 5
For what values of x in the matrix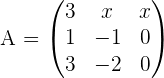
does the matrix inverse not support?
Solution of exercise 1
Calculate the matrix inverse by the gaussian elimination method.
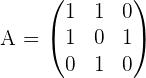
| r2 - r1 | r3 + r2 |
 |  |
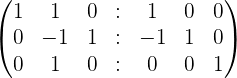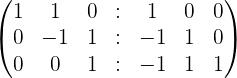| r2 - r3 | r1 + r2 |
 |  |
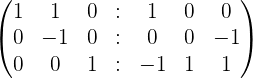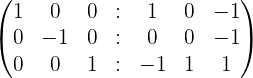| (-1) r2 | Matrix Inverse |
 |  |
Solution of exercise 2
Calculate the matrix inverse by the gaussian elimination method.
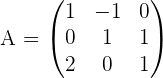
| r3 - 2r1 | r3 - 2r2 |
 |  |
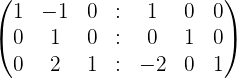| r1 + r2 | Matrix Inverse |
 |  |
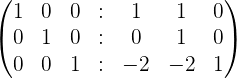Solution of exercise 3
Calculate the matrix inverse by determinants.
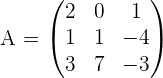
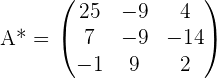
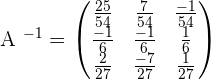
Solution of exercise 4
For what values of m in the matrix does not support an inverse?
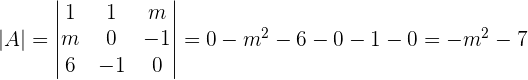
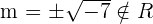
For any real value of m, there is the inverse 
.
Solution of exercise 5
For what values of x in the matrix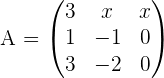
does the matrix inverse not support?
For x = 0 , Matrix A has no inverse.
Summarise with AI:
Did you like this article? Rate it!
Loading...
I appreciate your work, thanks so much keep up the good work ✅
Hello Little P! Thanks very much for the positive feedback!
I didn’t get the same answer for the second question, ive also asked my friends and we all got the same answer it just didnt line up with yours. Apart from that, great website and thanks for the exercises.
Very nice and good explanation of matrix
Give some more examples of matrix
I want to more study about matrix that’s why I’m using Google